设f(x)=x2+bx+c(b,c∈R).若|x|≥2时,f(x)≥0,且f(x)在区间(2,3]上的最大值为1,求b2+c2的最大值和最小值.
解:由题意函数图象为开口向上的抛物线,且f(x)在区间(2,3]上的最大值只能在闭端点取得,
故有f(2)≤f(3)=1,从而b≥-5且c=-3b-8.
若f(x)=0有实根,则△=b
2-4c=b
2+12b+32≥0,
∵|x|≥2时,f(x)≥0,
∴在区间[-2,2]有
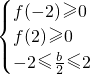
即
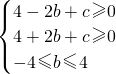
消去c,解出
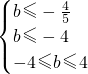
,
即b=-4,这时c=4,且△=0.
若f(x)=0无实根,则△=b
2-4c<0,将c=-3b-8代入解得-8<b<-4.
综上-5≤b≤-4.
所以b
2+c
2=b
2+(-3b-8)
2=10b
2+48b+64=10
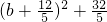
,
∴b
2+c
2在[-5,-4]上单调递减
故
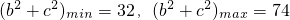
.
分析:根据题意函数图象为开口向上的抛物线,且f(x)在区间(2,3]上的最大值只能在闭端点取得,故有f(2)≤f(3)=1,从而b≥-5且c=-3b-8,再根据若|x|≥2时,f(x)≥0,可确定b的范围,进而可求b
2+c
2的最大值和最小值.
点评:本题是典型的二次函数最值问题,解题需要灵活运用初等数学思想,包括数形结合,分类讨论,函数思想,转化且探究意识要强.

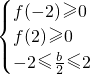 即
即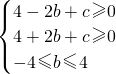 消去c,解出
消去c,解出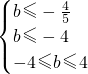 ,
,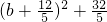 ,
,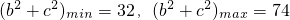 .
.
