
| A. | α+β<90° | B. | α+β≤90° | C. | α+β>90° | D. | α+β≥90° |
分析 根据线面角的定义分别作出α和β,结合三角形的边角关系进行判断即可.
解答 解:①若此直线与两个平面都相交,则:
设线段AB夹在直二面角α-l-β内,A∈α,B∈β,且设AB与平面α、β所成的角分别为α和β,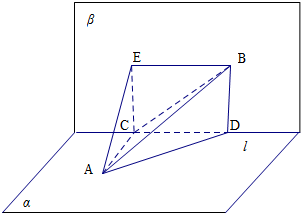
过A在α内做AC垂直于l于C点,过B在β内做BD垂直于l于D点.
在β内做BE平行l,在β内做CE平行BD,交点为E,连接AE,AD,BC
则∠DAB=α,∠ABC=β,sin∠ABC=$\frac{AC}{AB}$,sin∠ABD=$\frac{AD}{AB}$
∵AD>AC,∴∠ABC<∠ABD,
∵∠ABD+∠DAB=90°,∴α+β<90°
②当AB与l平行时:α+β=0°
③当AB与l垂直时:α+β=90°
综上所述:0°≤α+β≤90°,
故选:B
点评 本小题考查空间中的线面关系,直线与平面所成的角、二面角、解三角形等基础知识考查空间想象能力和思维能力.


科目:高中数学 来源: 题型:解答题
| 科目A | 科目B | 科目C | |
| 甲 | $\frac{2}{3}$ | $\frac{1}{2}$ | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
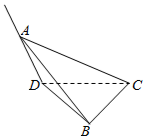 如图,在二面角A-CD-B中,BC⊥CD,BC=CD=2,点A在直线AD上运动,满足AD⊥CD,AB=3.现将平面ADC沿着CD进行翻折,在翻折的过程中,线段AD长的取值范围是$[\sqrt{5}-2,\sqrt{5}+2]$.
如图,在二面角A-CD-B中,BC⊥CD,BC=CD=2,点A在直线AD上运动,满足AD⊥CD,AB=3.现将平面ADC沿着CD进行翻折,在翻折的过程中,线段AD长的取值范围是$[\sqrt{5}-2,\sqrt{5}+2]$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ab>ac | B. | c(b-a)>0 | C. | ac(a-c)<0 | D. | cb2>ab2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ρcosθ=$\frac{1}{2}$ | B. | ρcosθ=2 | C. | ρ=4sin(θ+$\frac{π}{3}$) | D. | ρ=4sin(θ-$\frac{π}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,$\frac{1}{4}$) | B. | (-1,$\frac{1}{2}$)∪(1,+∞) | C. | (-∞,-1)∪(4,+∞) | D. | (-1,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 患病 | 未患病 | 总计 | |
| 未服用药 | 25 | 15 | 40 |
| 服用药 | c | d | 40 |
| 总计 | M | N | 80 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com