练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    判断下列两个试验是否为古典概型,并说明理由.

    (1)在线段［0,3］上任取一点,求此点的坐标小于1的概率;

    (2)从1,2,3,4四个数中任意取出两个数,求所取两数之一是2的概率.

    思路分析：根据古典概型的定义及特征进行判断.

    解:(1)在线段［0,3］上任取一点,此点可以在［0,3］上的任一位置,且在每个位置的可能性是相同的,具备等可能性.但试验的结果是无限多个,不满足古典概型的条件,即不满足试验结果的有限性.因此不属于古典概型.

    (2)此问题属于古典概型,因为此试验的所有基本事件共有6个:{1,2},{1,3},{1,4},{2,3},{2,4},{3,4},且每个事件的出现是等可能的,因此属于古典概型,所取两数之一是2的概率为P==.

    点评:判断一个概率模型是否为古典概型,就是看它是否符合古典概型的两个基本特征,即有限性和等可能性.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    下列说法中错误的是（　　）
    A、如果变量x与y之间存在着线性相关关系，则我们根据试验数据得到的点（xi，yi）（i=1，2，…，n）将散布在某一条直线的附近
    B、如果两个变量x与y之间不存在着线性关系，那么根据它们的一组数据（xi，yi）（i=1，2，…，n）不能写出一个线性方程
    C、设x，y是具有相关关系的两个变量，且x关于y的线性回归方程为
    ?
    y
    =bx+a，b叫做回归系数
    D、为使求出的线性回归方程有意义，可用统计检验的方法来判断变量y与x之间是否存在线性相关关系

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    判断下列各题中给出的事件是否是相互独立事件.

    （1）甲盒中有6个白球、4个黑球，乙盒中有3个白球、5个黑球.从甲盒中摸出一个球称为甲试验，从乙盒中摸出一个球称为乙试验.事件A1表示“从甲盒中取出的是白球”，事件B1表示“从乙盒中取出的是白球”.

    （2）盒中有4个白球、3个黑球，从盒中陆续取出两个球，用A2表示事件“第一次取出的是白球”,把取出的球放回盒中，用B2表示事件“第二次取出的是白球”.

    （3）盒中有4个白球、3个黑球，从盒中陆续取出两个球，用A3表示“第一次取出的是白球，”取出的球不放回，用B3表示“第二次取出的是白球”.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    下列说法中错误的是（    ）

           A．如果变量与之间存在着线性相关关系，则我们根据试验数据得到的点将散布在某一条直线的附近

           B．如果两个变量与之间不存在着线性关系，那么根据它们的一组数据不能写出一个线性方程

           C．设，是具有相关关系的两个变量，且关于的线性回归方程为， 叫做回归系数

           D．为使求出的线性回归方程有意义，可用统计检验的方法来判断变量与之间是否存在线性相关关系

    查看答案和解析>>

    科目：高中数学 来源：2009-2010学年度新课标高三上学期数学单元测试11-文科-统计案例、框图 题型：选择题

     下列说法中错误的是                 （    ）

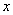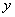        A．如果变量与之间存在着线性相关关系，则我们根据试验数据得到的点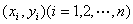将散布在某一条直线的附近

        B．如果两个变量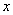与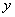之间不存在着线性关系，那么根据它们的一组数据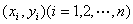不能写出一个线性方程

        C．设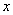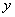，是具有相关关系的两个变量，且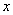关于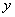的线性回归方程为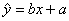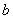， 叫做回归系数

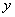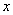        D．为使求出的线性回归方程有意义，可用统计检验的方法来判断变量与之间是否存

    在线性相关关系

     

    查看答案和解析>>

    同步练习册答案