
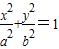 (a>b>0)的左、右焦点分别为F1,F2,已知椭圆E上的任意一点P,满足
(a>b>0)的左、右焦点分别为F1,F2,已知椭圆E上的任意一点P,满足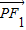 •
•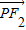 的最小值为
的最小值为 a2,过F1作垂直于椭圆长轴的弦长为3.
a2,过F1作垂直于椭圆长轴的弦长为3.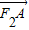 •
• 的取值范围.
的取值范围.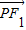 •
•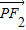 ,根据二次函数性质求得其最小值,令最小值为
,根据二次函数性质求得其最小值,令最小值为 a2,由长轴长可得
a2,由长轴长可得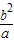 =
= ,结合a2=b2+c2即可解得a,b;
,结合a2=b2+c2即可解得a,b;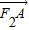 •
•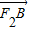 ;当过F1的直线AB存在斜率时,设斜率为k,则直线AB的方程为y=k(x+1),设A(x1,y1),B(x2,y2),联立直线方程与椭圆方程消去y得x的二次方程,利用韦达定理及向量数量积运算可把
;当过F1的直线AB存在斜率时,设斜率为k,则直线AB的方程为y=k(x+1),设A(x1,y1),B(x2,y2),联立直线方程与椭圆方程消去y得x的二次方程,利用韦达定理及向量数量积运算可把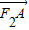 •
•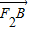 表示为关于k的函数,根据k的取值范围即可求得
表示为关于k的函数,根据k的取值范围即可求得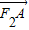 •
•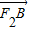 的范围,综上即可求得答案.
的范围,综上即可求得答案.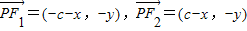 ,
,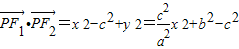 ,
,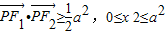 ,
,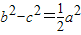 ,∴a=2c,
,∴a=2c, ,∴
,∴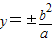 ,∴
,∴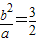 ,a2=4,b2=3,
,a2=4,b2=3,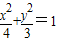 ;
; )B(-1,-
)B(-1,- ),则
),则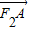 •
•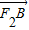 =
= ;
;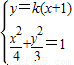 得:(4k2+3)x2+8k2x+4k2-12=0,
得:(4k2+3)x2+8k2x+4k2-12=0,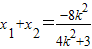 ,
,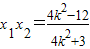 ,
,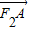 •
• =(x1-1)(x2-1)+y1y2=
=(x1-1)(x2-1)+y1y2=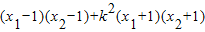
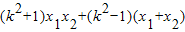 +(k2+1)=
+(k2+1)=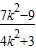 =
= -
-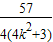 ,
,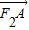 •
• <
< ,
, •
•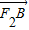 <
< ;
;

科目:高中数学 来源:山东省高考真题 题型:解答题
 (a,b>0)过M(2,
(a,b>0)过M(2,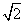 ),N(
),N( ,1)两点,O为坐标原点,
,1)两点,O为坐标原点, ?若存在,写出该圆的方程,并求|AB|的取值范围,若不存在,说明理由。
?若存在,写出该圆的方程,并求|AB|的取值范围,若不存在,说明理由。 查看答案和解析>>
科目:高中数学 来源:2009-2010学年黑龙江省鹤岗一中高二(上)期中数学试卷(文科)(解析版) 题型:解答题
 (a>b>0)过M(2,
(a>b>0)过M(2, ),N(
),N( ,1)两点,O为坐标原点,
,1)两点,O为坐标原点, ?若存在,写出该圆的方程,并求|AB|取值范围;若不存在,说明理由.
?若存在,写出该圆的方程,并求|AB|取值范围;若不存在,说明理由.查看答案和解析>>
科目:高中数学 来源:2011-2012学年安徽省安庆市枞阳三中高二(上)第二次段考数学试卷(解析版) 题型:解答题
 (a>b>0)过M(2,
(a>b>0)过M(2, ),N(
),N( ,1)两点,O为坐标原点,
,1)两点,O为坐标原点, ?若存在,写出该圆的方程,并求|AB|取值范围;若不存在,说明理由.
?若存在,写出该圆的方程,并求|AB|取值范围;若不存在,说明理由.查看答案和解析>>
科目:高中数学 来源:2009-2010学年重庆市西南师大附中高二(上)期中数学试卷(解析版) 题型:解答题
 (a>b>0)过M(2,
(a>b>0)过M(2, ),N(
),N( ,1)两点,O为坐标原点,
,1)两点,O为坐标原点, ?若存在,写出该圆的方程,并求|AB|取值范围;若不存在,说明理由.
?若存在,写出该圆的方程,并求|AB|取值范围;若不存在,说明理由.查看答案和解析>>
科目:高中数学 来源:2011-2012学年安徽省皖北协作区高三(下)3月联考数学试卷(理科)(解析版) 题型:解答题
 (a>b>0)过M(2,
(a>b>0)过M(2, ),N(
),N( ,1)两点,O为坐标原点,
,1)两点,O为坐标原点, ?若存在,写出该圆的方程,并求|AB|取值范围;若不存在,说明理由.
?若存在,写出该圆的方程,并求|AB|取值范围;若不存在,说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com