
(1)用a、b表示向量![]() ;
;
(2)设|a|=1,|b|=2,|![]() |∈[2
|∈[2![]() ,2
,2![]() ],求a与b的夹角θ的取值范围.
],求a与b的夹角θ的取值范围.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源:选修设计数学A4-1人教版 人教版 题型:022
用符号语言表述是:已知a∥b∥c,直线m、n分别与a、b、c交于点A、B、C和![]() 、
、![]() 、
、![]() (如图),如果________,那么________.
(如图),如果________,那么________.
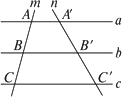
对于定理的证明,分m平行于n和m不平行于n两种情况证明.当m平行于n时,直接运用平行四边形加以证明;当m不平行于n时,利用辅助线构造相似三角形,进而关系式得证.
查看答案和解析>>
科目:高中数学 来源:2013届广东省汕头市高三上学期期中理科数学试卷(解析版) 题型:选择题
对于下列命题:①在△ABC中,若 ,则△ABC为等腰三角形;②已知a, b,c是△ABC的三边长,若
,则△ABC为等腰三角形;②已知a, b,c是△ABC的三边长,若 ,
, ,
, ,则△ABC有两组解;③设
,则△ABC有两组解;③设 ,
, ,
, ,则
,则 ;④将函数
;④将函数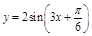 图象向左平移
图象向左平移 个单位,得到函数
个单位,得到函数 图象。其中正确命题的个数是( )
图象。其中正确命题的个数是( )
A.  B.
B.
 C.
C.  D.
D.

查看答案和解析>>
科目:高中数学 来源: 题型:
给出如下4个命题:①若α.β是两个不重合的平面,![]() .m是两条不重合的直线,则α∥β的一个充分而不必要条件是
.m是两条不重合的直线,则α∥β的一个充分而不必要条件是![]() ⊥α,m⊥β,且
⊥α,m⊥β,且![]() ∥m;②对于任意一条直线a,平面α内必有无数条直线与a垂直;③已知命题P:若四点不共面,那么这四点中任何三点都不共线.而命题P的逆否命题是假命题;④已知a.b.c.d是四条不重合的直线,如果a⊥c,a⊥d,b⊥c,b⊥d,则“a∥b”与“c∥d”不可能都不成立.在以上4个命题中,正确命题的序号是__▲____. (要求将所有你认为正确的命题序号都填上)
∥m;②对于任意一条直线a,平面α内必有无数条直线与a垂直;③已知命题P:若四点不共面,那么这四点中任何三点都不共线.而命题P的逆否命题是假命题;④已知a.b.c.d是四条不重合的直线,如果a⊥c,a⊥d,b⊥c,b⊥d,则“a∥b”与“c∥d”不可能都不成立.在以上4个命题中,正确命题的序号是__▲____. (要求将所有你认为正确的命题序号都填上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com