
分析 (1)由已知中f(-2)=f(4),可得函数图象的对称轴为直线x=1,结合函数f(x)最大值为2,设出函数的顶点式,进而可得答案;
(2)分析给定区间[t,t+1]与对称轴的位置,进而得到函数的在[t,t+1]上的单调性和最大值.
解答 解:(1)因为f(-2)=f(4),
所以函数图象的对称轴为直线x=1,
又因为f(x)max=2,
所以设f(x)=a(x-1)2+2,a<0,
由f(-2)=a(-2-1)2+2=-16得a=-2,
所以f(x)=-2(x-1)2+2=-2x2+4x,
即所求函数y=f(x)的解析式为f(x)=-2x2+4x.
(2)①当t+1≤1即t≤0时,
y=f(x)在[t,t+1]上单调递增,
所以f(x)max=f(t+1)=-2(t+1-1)2+2=-2t2+2;
②当t≥1时,y=f(x)在[t,t+1]上单调递减,
所以f(x)max=f(t)=-2(t-1)2+2=-2t2+4t;
③当t<1<t+1即0<t<1时,y=f(x)在[t,1]上单调递增,在[1,t+1]上单调递减,
所以f(x)max=f(1)=-2(1-1)2+2=2.
综上所述,f(x)max=$\left\{\begin{array}{l}-2{t}^{2}+2,t≤0\\ 2,0<t<1\\-2{t}^{2}+4t,t≥1\end{array}\right.$
点评 本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质,是解答的关键.


 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:高中数学 来源: 题型:解答题
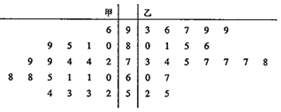
| 甲班 | 乙班 | 总计 | |
| 成绩优良 | |||
| 成绩不优良 | |||
| 总计 |
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
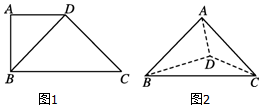 如图1所示,在四边形ABCD中,AD∥BC,AD=AB=1,∠BCD=45°,∠BAD=90°.将△ADB沿BD折起,使平面ABD⊥平面BCD,构成三棱锥ABCD(如图2)
如图1所示,在四边形ABCD中,AD∥BC,AD=AB=1,∠BCD=45°,∠BAD=90°.将△ADB沿BD折起,使平面ABD⊥平面BCD,构成三棱锥ABCD(如图2)查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,3] | B. | [-1,2] | C. | (1,2] | D. | [1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若 m∥n,m⊥α,n⊥β,则α∥β | B. | 若m∥α,α∩β=n,则m∥n | ||
| C. | 若m⊥α,α∥β,则m⊥β | D. | 若m⊥α,n⊥β,m⊥n,则α⊥β |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 货物 | 体积(m3/箱) | 重量(50kg/箱) | 利润(百元/箱) |
| 甲 | 5 | 2 | 20 |
| 乙 | 4 | 5 | 10 |
| 托运限制 | 24 | 13 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com