Question

已知常数c、d都是实数,在数列{a_n}与{b_n}中,a₁=0,b₁=1.对任何正整数n,等式a_n+1=ca_n+d,b_n+1=cb_n+d都成立.

(1)当c=1时,求数列{a_n}与{b_n}的通项公式;

(2)当c＞0且c≠1时,要使数列{b_n}是公比不为1的等比数列,求d的值;

(3)当c＞0时,设数列{a_n}的前n项和、{b_n}的前n项和分别为S_n与T_n,求(T₁+T₂+…+T₁₀₀)-(S₁+S₂+…+S₁₀₀)的值.

Answer 1

解:(1)∵c=1＞0,∴a_n=c·a_n-1+d=a_n-1+d,b_n=b_n-1+d(n≥2).

∴{a_n}、{b_n}都是公差为d的等差数列.∵a₁=0,b₁=1,∴a_n=(n-1)d,b_n=1+(n-1)d(n∈N^*).

(2)∵c＞0,∴b_n=cb_n-1+d.∴=c+.∵{b_n}是等比数列,∴为常数.

∵{b_n}是公比不为1的等比数列,∴b_n-1不是常数.∴必有d=0.

(3)∵c＞0,∴a_n=c·a_n-1+d,b_n=c·b_n-1+d.两式相减得:b_n-a_n=c(b_n-1-a_n-1)(n≥2),

∴{b_n-a_n}为等比数列.∴b_n-a_n=(b₁-a₁)c^n-1=c^n-1.

∴T_n-S_n=(b₁-a₁)+(b₂-a₂)+…+(b_n-a_n)=1+c+c²+…+c^n-1=n,c=1,

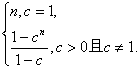,c＞0且c≠1.

∴当c=1时,(T₁+T₂+…+T₁₀₀)-(S₁+S₂+…+S₁₀₀)

=(T₁-S₁)+(T₂-S₂)+…+(T₁₀₀-S₁₀₀)

=1+2+3+…+100==5 050.

∴当c＞0且c≠1时,(T₁+T₂+…+T₁₀₀)-(S₁+S₂+…+S₁₀₀)

=(T₁-S₁)+(T₂-S₂)+…+(T₁₀₀-S₁₀₀)

=++…+=［100］=.