解:(Ⅰ)由题知:g(x)=

x
2-2x+2+lnx的定义域为(0,+∞)

当g′(x)>0,即0<x<

或x>2时,函数g(x)为增函数;
当g′(x)<0,即

<x<2时,函数g(x)为减函数.
所以,g(x)的单调递增区间为(0,

)∪(2,+∞),单调递减区间为(

,2)
(Ⅱ)∵g(x)在(2,+∞)上为增函数,在(

,2)上为减函数,
∴g(x)在x∈
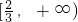
上的最小值为g(2)
且g(2)=
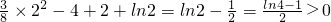
∴g(x)在x∈
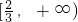
上没有零点,
∴要想使函数g(x)在[e
n,+∞)(n∈Z)上有零点,并考虑到g(x)在(0,

)单调递增且在(

,2)单调递减,故只须

且g(e
n)≤0即可,
易验证
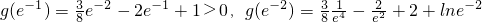
=
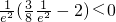
,
根据g(x)在(0,

)为单调递增函数,当n≤-2且n∈Z时均有g(e
n)≤g(e
-2)<0,
即函数g(x)在[e
n,e
-1]?[e
n,+∞)(n∈Z)上有零点
∴n的最大值为-2.
分析:(1)令g′(x)>0,得到g(x)的单调增区间;令g′(x)<0,得到g(x)的单调减区间.
(2)容易求得g(x)在[

,+∞]的最小值为g(2)大于0,若g(x)在[e
n,+∞)(n∈Z)上有零点,只能在(0,

)上存在零点,故只须令e
n<

且g(e
n)≤0,找到n的最大值即可.
点评:本题较好,是关于函数的综合题,主要考查函数的单调性、最值、零点等函数的基本知识,应熟练掌握.

 ,
,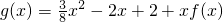 .
. x2-2x+2+lnx的定义域为(0,+∞)
x2-2x+2+lnx的定义域为(0,+∞)
 或x>2时,函数g(x)为增函数;
或x>2时,函数g(x)为增函数; <x<2时,函数g(x)为减函数.
<x<2时,函数g(x)为减函数. )∪(2,+∞),单调递减区间为(
)∪(2,+∞),单调递减区间为( ,2)
,2) ,2)上为减函数,
,2)上为减函数,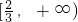 上的最小值为g(2)
上的最小值为g(2)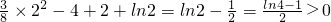
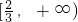 上没有零点,
上没有零点, )单调递增且在(
)单调递增且在( ,2)单调递减,故只须
,2)单调递减,故只须 且g(en)≤0即可,
且g(en)≤0即可,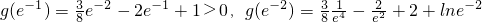 =
=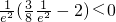 ,
, )为单调递增函数,当n≤-2且n∈Z时均有g(en)≤g(e-2)<0,
)为单调递增函数,当n≤-2且n∈Z时均有g(en)≤g(e-2)<0, ,+∞]的最小值为g(2)大于0,若g(x)在[en,+∞)(n∈Z)上有零点,只能在(0,
,+∞]的最小值为g(2)大于0,若g(x)在[en,+∞)(n∈Z)上有零点,只能在(0, )上存在零点,故只须令en<
)上存在零点,故只须令en< 且g(en)≤0,找到n的最大值即可.
且g(en)≤0,找到n的最大值即可.

 阅读快车系列答案
阅读快车系列答案