练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
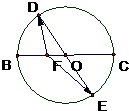
    如图，BC、DE是半径为1的圆O的两条直径，
    BF
    =2
    FO
    ，则
    FD
    •
    FE
    =
    -
    8
    9
    -
    8
    9
    ．
    分析：由
    BF
    =2
    FO
    ，及
    BF
    +
    FO
    =
    BO
    ，可计算出向量
    FO
    的模；再利用向量的加法法则可得：
    FD
    =
    FO
    +
    OD
    ，
    FE
    =
    FO
    +
    OE
    ，根据数量积的运算法则即可计算出．
    解答：解：∵
    BF
    =2
    FO
    ，r=1，∴|
    FO
    |=
    1
    3
    ．
    ∴
    FD
    •
    FE
    =(
    FO
    +
    OD
    )•(
    FO
    +
    OE
    )    =
    FO
    2    +
    FO
    •(
    OE
    +
    OD
    )+
    OD
    •
    OE
    =(
    1
    3
    )2+0-r2    =
    1
    9
    -1=-
    8
    9
    ．
    故答案为-
    8
    9
    ．
    点评：充分理解向量的运算法则和数量积的定义是解题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    A．选修4-1：几何证明选讲
    如图，直角△ABC中，∠B=90°，以BC为直径的⊙O交AC于点D，点E是AB的中点．
    求证：DE是⊙O的切线．
    B．选修4-2：矩阵与变换
    已知二阶矩阵A有特征值-1及其对应的一个特征向量为
    1
    -4
    ，点P（2，-1）在矩阵A对应的变换下得到点P′（5，1），求矩阵A．
    C．选修4-4：坐标系与参数方程
    在直角坐标系中，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系．已知直线l的极坐标方程为ρcos(θ-
    π
    4
    )=
    		2
    ，曲线C的参数方程为
    x=2cosα
    y=sinα
    （α为参数），求曲线C截直线l所得的弦长．
    D．选修4-5：不等式选讲
    已知a，b，c都是正数，且abc=8，求证：log2（2+a）+log2（2+b）+log2（2+c）≥6．

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年江苏省盐城市东台一中、时堰中学、唐洋中学高三（上）期中数学试卷（解析版） 题型：解答题

    A．选修4-1：几何证明选讲
    如图，直角△ABC中，∠B=90°，以BC为直径的⊙O交AC于点D，点E是AB的中点．
    求证：DE是⊙O的切线．
    B．选修4-2：矩阵与变换
    已知二阶矩阵A有特征值-1及其对应的一个特征向量为，点P（2，-1）在矩阵A对应的变换下得到点P′（5，1），求矩阵A．
    C．选修4-4：坐标系与参数方程
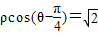    在直角坐标系中，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系．已知直线l的极坐标方程为，曲线C的参数方程为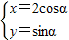（α为参数），求曲线C截直线l所得的弦长．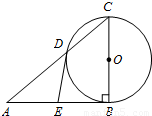
    D．选修4-5：不等式选讲
    已知a，b，c都是正数，且abc=8，求证：log2（2+a）+log2（2+b）+log2（2+c）≥6．

    查看答案和解析>>

    同步练习册答案