
(09年临沂一模文)(12分)
如图,PA⊥平面ABCD,ABCD是矩形,PA=AB=1,AD=![]() ,点F是PB的中点,点E在边BC上移动。
,点F是PB的中点,点E在边BC上移动。
(1)求三棱锥E-PAD的体积;
(2)当点E为BC的中点时,试判断EF与平面PAC的位置关系,并说明理由;
(3)证明:无论点E在边BC的何处,都有PE⊥AF。

解析:(1)∵PA⊥平面ABCD,ABCD为矩形,
![]() ┉┉┉┉┉┉┉┉2分
┉┉┉┉┉┉┉┉2分
=![]() =
=![]() ┉┉┉┉┉┉┉┉4分
┉┉┉┉┉┉┉┉4分
(2)当E为BC中点时,∵F为PB的中点,
∴EF∥PC ┉┉┉┉┉┉┉┉5分
∵EF![]() 平面PAC,PC
平面PAC,PC![]() 平面PAC,
平面PAC,
∴EF∥平面PAC,即EF与平面PAC平行。┉┉┉┉┉┉┉┉8分
(3)∵PA=AB,F为PB的中点,
∴AF⊥PB ┉┉┉┉┉┉┉┉9分
∵PA⊥平面ABCD, ∴PA⊥BC
又BC⊥AB,BC⊥平面PAB
又AF![]() 平面PAB
平面PAB
∴BC⊥AF。 ┉┉┉┉┉┉┉┉10分
又PB∩BC=B, ∴AF⊥平面PBC ┉┉┉┉┉┉┉┉11分
因无论点E在边BC的何处,都有PE![]() 平面PBC,
平面PBC,
∴AF⊥PE。 ┉┉┉┉┉┉┉┉12分


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
(09年临沂一模文)(14分)
已知函数![]() .
.
(1) 当a=-3时,求函数f(x)的极值;
(2) 若函数f(x)的图象与x轴有三个不同的交点,求a的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
(09年临沂一模文)(12分)
已知F1,F2是椭圆C: ![]() (a>b>0)的左、右焦点,点P
(a>b>0)的左、右焦点,点P![]() 在椭圆上,线段PF2与y轴的交点M满足
在椭圆上,线段PF2与y轴的交点M满足![]() 。
。
(1)求椭圆C的方程。
(2)椭圆C上任一动点M![]() 关于直线y=2x的对称点为M1(x1,y1),求3x1-4y1的取值范围。
关于直线y=2x的对称点为M1(x1,y1),求3x1-4y1的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
(09年临沂一模文)(12分)
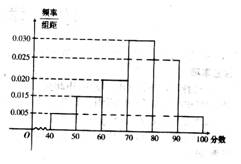
某校从参加高二年级学业水平测试的学生中抽出80名学生,其数学成绩(均为整数)的频率分布直方图如图所示。
(1)估计这次测试数学成绩的平均分;
(2)假设在[90,100]段的学生的数学成绩都不相同,且都在94分以上,现用简单随机抽样的方法,从95,96,97,98,99,100这6个数中任取2个数,求这两个数恰好是在[90,100]段的两个学生的数学成绩的概率。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com