
 、
、 是不全为零的实数,试比较
是不全为零的实数,试比较 与
与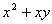 的大小;
的大小; 为正数,且
为正数,且 ,求证:
,求证: .
. ;(2)证明见解析.
;(2)证明见解析.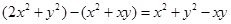 ,下面就是确定
,下面就是确定 与0的大小,
与0的大小, 是一个二次三项式,因此我们可用配方法配方,
是一个二次三项式,因此我们可用配方法配方,
 ,由于
,由于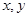 不全为零,因此
不全为零,因此 ,从而有
,从而有
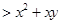 ;另外本题实质是比较
;另外本题实质是比较 与
与 的大小,想到基本不等式,有
的大小,想到基本不等式,有 (
( 时取等号),而
时取等号),而 ,再讨论下等号能否成立即可;(2)这是条件不等式的证明,而且已知与求证式都是对称式,因此大胆想象等号成立时,各字母应该相等,事实上也正是在
,再讨论下等号能否成立即可;(2)这是条件不等式的证明,而且已知与求证式都是对称式,因此大胆想象等号成立时,各字母应该相等,事实上也正是在 时取等号,接下来考虑不等式的证明,关键是条件怎么应用,这里我们偿试把
时取等号,接下来考虑不等式的证明,关键是条件怎么应用,这里我们偿试把 中的分子的1全部用
中的分子的1全部用 代换 ,有
代换 ,有
 ,把这个分式展开重新分组为
,把这个分式展开重新分组为
 ,下面易证.
,下面易证. -
- =
= =
= 3分
3分 、
、 是不全为零的实数,所以
是不全为零的实数,所以 ,即
,即 >
>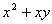 。 6分
。 6分 时,
时, 
 ; 2分
; 2分 时,作差:
时,作差:
 ;
; 、
、 是不全为零的实数,所以当
是不全为零的实数,所以当 时,
时, >
>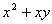 。
。 >
>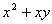 。 6分
。 6分 时,取得等号3。 7分
时,取得等号3。 7分


 .
. 14分
14分

 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:高中数学 来源:不详 题型:解答题
 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
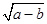 >
>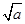 -
-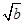 ;④a3+b3>2a2b.其中一定成立的不等式序号为________.
;④a3+b3>2a2b.其中一定成立的不等式序号为________.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com