

 ,利用函数的单调性即可求得实数a的值.
,利用函数的单调性即可求得实数a的值. (0<x≤1),
(0<x≤1), ,则f(x)在(0,1]上单调递减,
,则f(x)在(0,1]上单调递减,
 .①
.① .②
.② .
. .
.

科目:高中数学 来源: 题型:
| 10 |
| 7 |
A、(
| ||
B、(-∞,
| ||
C、(-
| ||
D、(-∞,-
|
查看答案和解析>>
科目:高中数学 来源:2014届新课标高二下学期期中考试文科数学试卷(解析版) 题型:解答题
(满分12分)写出命题:“已知a,x为实数,如果关于x的不等式x2+(2a+1)x+a2+2≤0的解集非空,则a≥1”的逆命题,否命题,逆否命题并判断其真假。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2011年高三数学复习(第5章 不等式):5.7 有理不等式解法(解析版) 题型:选择题
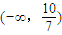 ,则关于x的不等式ax>b的解集是( )
,则关于x的不等式ax>b的解集是( )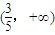
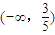
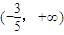
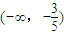
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com