
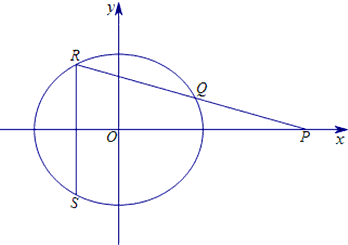
 已知椭圆
已知椭圆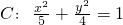 的右焦点为F,过点P(5,0)的直线l与椭圆C交于Q、R,且
的右焦点为F,过点P(5,0)的直线l与椭圆C交于Q、R,且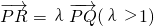 .
. ,求直线l的方程;
,求直线l的方程;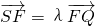 .
. ,∴(x1-5,y1)=
,∴(x1-5,y1)= (x2-5,y2)
(x2-5,y2) x2-
x2- ,y1=
,y1= y2,
y2, ,
,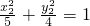
 ,
,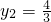

 (x-5);
(x-5);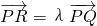 ,∴(x1-5,y1)=λ(x2-5,y2)
,∴(x1-5,y1)=λ(x2-5,y2) ,
,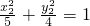
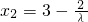
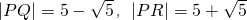 ,
,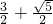
 =(1-x1,y1),
=(1-x1,y1), =(x2-1,y2),
=(x2-1,y2),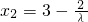
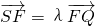
 ,可得坐标之间的关系,再利用点在椭圆上,求得点的坐标,即可求得直线l的方程;
,可得坐标之间的关系,再利用点在椭圆上,求得点的坐标,即可求得直线l的方程;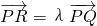 ,可得坐标之间的关系,再利用点在椭圆上,求得点的坐标,当且仅当P,Q,R在长轴上时,λ最大;
,可得坐标之间的关系,再利用点在椭圆上,求得点的坐标,当且仅当P,Q,R在长轴上时,λ最大;

 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中数学 来源: 题型:
| AC |
A、
| ||
| B、2 | ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年黄冈中学二模理)如图,已知椭圆![]() 的右焦点为F,过F的直线(非x轴)交椭圆于M、N两点,右准线
的右焦点为F,过F的直线(非x轴)交椭圆于M、N两点,右准线![]() 交x轴于点K,左顶点为A.
交x轴于点K,左顶点为A.
(1)求证:KF平分∠MKN;
(2)直线AM、AN分别交准线![]() 于点P、Q,设直线MN的倾斜角为
于点P、Q,设直线MN的倾斜角为![]() ,试用
,试用![]() 表示线段PQ的长度|PQ|,并求|PQ|的最小值.
表示线段PQ的长度|PQ|,并求|PQ|的最小值.

查看答案和解析>>
科目:高中数学 来源: 题型:
(14分)已知椭圆![]() 的右焦点为F,上顶点为A,P为C
的右焦点为F,上顶点为A,P为C![]() 上任一点,MN是圆
上任一点,MN是圆![]() 的一条直径,若与AF平行且在y轴上的截距为
的一条直径,若与AF平行且在y轴上的截距为![]() 的直线
的直线![]() 恰好与圆
恰好与圆![]() 相切。
相切。
(1)已知椭圆![]() 的离心率;
的离心率;
(2)若![]() 的最大值为49,求椭圆C
的最大值为49,求椭圆C![]() 的方程。
的方程。
查看答案和解析>>
科目:高中数学 来源:2010年普通高等学校招生全国统一考试(重庆卷)数学理工类模拟试卷(三) 题型:解答题
如图,已知椭圆 的右焦点为F,过F的直线(非x轴)交椭圆于M、N两点,右准线
的右焦点为F,过F的直线(非x轴)交椭圆于M、N两点,右准线 交x轴于点K,左顶点为A.
交x轴于点K,左顶点为A.
(Ⅰ)求证:KF平分∠MKN;
(Ⅱ)直线AM、AN分别交准线 于点P、Q,
于点P、Q,
设直线MN的倾斜角为 ,试用
,试用 表示
表示
线段PQ的长度|PQ|,并求|PQ|的最小值.
查看答案和解析>>
科目:高中数学 来源:2010年广东省高考冲刺强化训练试卷十三文科数学 题型:解答题
(本小题满分14分)已知椭圆 的右焦点为F,上顶点为A,P为C
的右焦点为F,上顶点为A,P为C 上任一点,MN是圆
上任一点,MN是圆 的一条直径,若与AF平行且在y轴上的截距为
的一条直径,若与AF平行且在y轴上的截距为 的直线
的直线 恰好与圆
恰好与圆 相切.
相切.
(Ⅰ)求椭圆 的离心率;
的离心率;
(Ⅱ)若 的最大值为49,求椭圆C
的最大值为49,求椭圆C 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com