
| A. | $\sqrt{3}$akm | B. | 2akm | C. | $\sqrt{5}$akm | D. | $\sqrt{7}$akm |
 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源: 题型:填空题
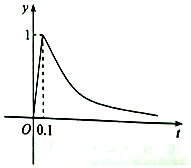 雾霾是人体健康的隐形杀手,爱护环境,人人有责.某环保实验室在雾霾天采用清洁剂处理教室空气质量.实验发现,当在教室释放清洁剂的过程中,空气中清洁剂的含剂浓度y(mg/m3)与时间t(h)成正比;释放完毕后,y与t的函数关系为y=($\frac{1}{16}$)t-a(a为常数),如图,已知当教室的空气中含剂浓度在0.25mg/m3以上时,教室最适合人体活动.根据图中信息,从一次释放清洁剂开始,这间教室有0.575h最适合人体活动.
雾霾是人体健康的隐形杀手,爱护环境,人人有责.某环保实验室在雾霾天采用清洁剂处理教室空气质量.实验发现,当在教室释放清洁剂的过程中,空气中清洁剂的含剂浓度y(mg/m3)与时间t(h)成正比;释放完毕后,y与t的函数关系为y=($\frac{1}{16}$)t-a(a为常数),如图,已知当教室的空气中含剂浓度在0.25mg/m3以上时,教室最适合人体活动.根据图中信息,从一次释放清洁剂开始,这间教室有0.575h最适合人体活动.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
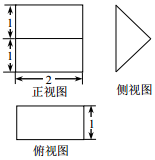 《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示,则该“堑堵”的表面积为( )
《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示,则该“堑堵”的表面积为( )| A. | 4 | B. | $6+4\sqrt{2}$ | C. | $4+4\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 16 | B. | 24 | C. | 32 | D. | 40 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=($\frac{1}{2}$)x | B. | y=x-2 | C. | y=x2+1 | D. | y=log3(-x) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com