
(本小题两小题,每题6分,满分12分)
⑴对任意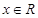 ,试比较
,试比较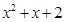 与
与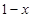 的大小;
的大小;
⑵已知函数 的定义域为R,求实数k的取值范围。
的定义域为R,求实数k的取值范围。
⑴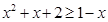 。 ⑵
。 ⑵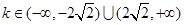
【解析】
试题分析:(1)根据作差法比较大小是一种重要的方法。同时要注意差式的变形技巧的运用。
(2)利用对数函数定义域为R,说明了无论x取什么样的数,表达式真数恒大于零,那么说明二次函数开口向上,判别式小于零得到。
⑴∵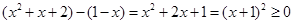 ,∴
,∴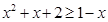 。
。
⑵∵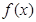 的定义域为
的定义域为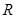 ,即
,即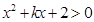 恒成立,∴
恒成立,∴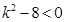 ,
,
即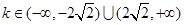
考点:本题主要考查配方法的运用,为判定差是大于零还是小于零,配方法也是常用的方法之一,比差法是比较两个代数式值的大小的常用方法,此题正是有效地利用了这两个方法,使问题得到解决,同时也考查了函数的定义域为R的理解和运用。
点评:解决该试题的关键是要比较两式的大小,可以运用比差法,把两个式子相减,可以得运用配方法来比较与零的大小关系,要使得对数函数定义域为R,说明了对数的真数部分恒大于零。


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
|
|
| π |
| 3 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年海南省嘉积中学高二下学期教学质量检测(三)数学(理) 题型:解答题
(本小题满分12分) 甲、乙两人参加某电视台举办的答题闯关游戏,按照规则,
甲先从 道备选题中一次性抽取
道备选题中一次性抽取 道题独立作答,然后由乙回答剩余
道题独立作答,然后由乙回答剩余 题,每人答对其中
题,每人答对其中
题就停止答题,即闯关成功.已知在 道备选题中,甲能答对其中的
道备选题中,甲能答对其中的 道题,乙答对每道题
道题,乙答对每道题
的概率都是 .
.
(Ⅰ)求甲、乙至少有一人闯关成功的概率;
(Ⅱ)设甲答对题目的个数为ξ,求ξ的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年高三一轮精品复习单元测试(11)数学试卷解析版 题型:解答题
(本小题满分12分)袋中装有黑球和白球共7个,从中任取2个球都是白球的概率为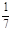 .现有甲、乙两人从袋中轮流摸取1个球,甲先取,乙后取,然后甲再取,
.现有甲、乙两人从袋中轮流摸取1个球,甲先取,乙后取,然后甲再取,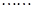 ,取后不放回,直到两人中有一人取到白球时即终止,每个球在每一次被取出的机会是等可能的.求:
,取后不放回,直到两人中有一人取到白球时即终止,每个球在每一次被取出的机会是等可能的.求:
(1)则袋中原有白球的个数;
(2)取球2次终止的概率;
(3)甲取到白球的概率
查看答案和解析>>
科目:高中数学 来源:正定中学2010高三下学期第一次考试(数学理) 题型:解答题
(本小题满分12分)
一次考试共有12道选择题,每道选择题都有4个选项,其中有且只有一个是正确的.评
分标准规定:“每题只选一个选项,答对得5分,不答或答错得零分”.某考生已确定
有8道题的答案是正确的,其余题中:有两道题都可判断两个选项是错误的,有一道
题可以判断一个选项是错误的,还有一道题因不理解题意只好乱猜.请求出该考生:
(1)得60分的概率;
(2)得多少分的可能性最大?
(3)所得分数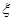 的数学期望(用分数表示,精确到0.01).
的数学期望(用分数表示,精确到0.01).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com