练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设函数是实常数, 如果函数在区间(-1, 1)上有

    零点, 求a的取值范围.

    解析:当a=0时, 则f(x)=4x-3, 此时f(x)的零点为∈(-1, 1), 故a=0满足题设.

       当a≠0时, 令△=16+8a(3+a)=0, 即a2+3a+2=0 解得a= -1或-2

       (1)当a= -1时, 此时f(x)= -2x2+4x-2= -2(x-1)2, 它有一个零点-1Ï(-1, 1)

         当a= -2时, 此时f(x)= -4x2+4x-1= -4(x-)2, 它有一个零点∈( -1, 1),

         故 a= -2满足题设

       (2)当f(-1)f(1)= (a-7)( a+1)＜0即 -1＜a＜7时, f(x)有唯一一个零点在(-1, 1)内

       (3)当f(x)在(-1, 1)上有两个零点时, 则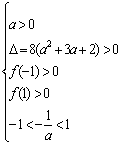或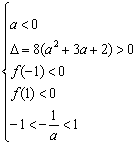

          解得a＞7或a＜-2

       综上所述, a的取值范围是a≤-2或-1＜a＜7或a＞7

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （本小题满分14分）如果对于函数的定义域内任意的，都有成立，那么就称函数是定义域上的“平缓函数”．

    （1）判断函数，是否是“平缓函数”；（2）若函数是闭区间上的“平缓函数”，且．证明：对于任意的，都有成立．（3）设、为实常数，．若是区间上的“平缓函数”，试估计的取值范围（用表示，不必证明）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如果对于函数的定义域内任意的，都有成立，那么就称函数是定义域上的“平缓函数”．（1）判断函数，是否是“平缓函数”；（2）若函数是闭区间上的“平缓函数”，且．证明：对于任意的，都有成立．（3）设、为实常数，．若是区间上的“平缓函数”，试估计的取值范围（用表示，不必证明）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

      (本小题13分) 是等差数列的前项和，.

    （Ⅰ）求的通项公式;

    （Ⅱ）设（是实常数，且），求的前项和.

    查看答案和解析>>

    科目：高中数学 来源：2009年上海市青浦区高考数学一模试卷（解析版） 题型：解答题

    设函数为实常数）在区间上的最小值为-4，那么a的值为    ．

    查看答案和解析>>

    同步练习册答案