
 [a2x+2(ab)x-b2x+1](a、b∈R+),如何求使y为负值的x的取值范围?
[a2x+2(ab)x-b2x+1](a、b∈R+),如何求使y为负值的x的取值范围? )2x+2(
)2x+2( )x-1>0
)x-1>0 )x>
)x> -1或(
-1或( )x<-
)x<- -1(舍去)
-1(舍去)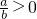 .
. >1时,即a>b>0时,x>lo
>1时,即a>b>0时,x>lo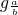 (
( -1).
-1). =1时,即a=b>0时,x∈R.
=1时,即a=b>0时,x∈R. <1时,即0<a<b时,x<lo
<1时,即0<a<b时,x<lo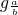 (
( -1)
-1)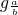 (
( -1);当a=b>0时,x∈R;当0<a<b时,x<lo
-1);当a=b>0时,x∈R;当0<a<b时,x<lo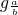 (
( -1).
-1). )x>
)x> -1或(
-1或( )x<-
)x<- -1(舍去)后,再分
-1(舍去)后,再分 >1,
>1, =1,
=1, <1三种情况进行讨论,从而求出使y为负值的x的取值范围.
<1三种情况进行讨论,从而求出使y为负值的x的取值范围.

科目:高中数学 来源:2006年高考第一轮复习数学:2.8 对数与对数函数(解析版) 题型:解答题
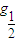 [a2x+2(ab)x-b2x+1](a、b∈R+),如何求使y为负值的x的取值范围?
[a2x+2(ab)x-b2x+1](a、b∈R+),如何求使y为负值的x的取值范围?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com