Question

9．已知F为抛物线y²=4x的焦点，点A，B在该抛物线上，$\overrightarrow{OA}$$•\overrightarrow{OB}$=0（其中O为坐标原点），则△ABO与△BFO面积之差的最小值是（　　）

• A． 4
• B． 8
• C． 8$\sqrt{3}$
• D． 16$\sqrt{3}$

Answer 1

分析 设出A，B的坐标，讨论直线斜率存在时，联立直线方程与抛物线方程，利用消元法得到关于x的一元二次方程，由$\overrightarrow{OA}$$•\overrightarrow{OB}$=0，得x₁x₂+y₁y₂=0，建立关于参数k，b的关系，消去b可得直线恒过（4，0），再考虑斜率不存在，结论成立，即可得出结论．

解答 解：设点A，B的坐标分别为（x₁，y₁），（x₂，y₂），设A在上方，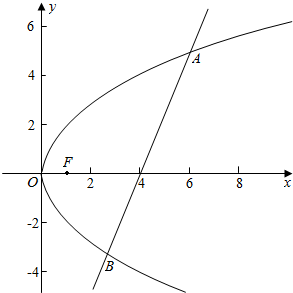

（1）当直线l存在斜率时，设直线方程为y=kx+b，显然k≠0且b≠0．
联立方程，消去y得k²x²+（2kb-4）x+b²=0①，则x₁x₂=$\frac{{b}^{2}}{{k}^{2}}$，
由y₁²=4x₁，y₂²=4x₂，则y₁y₂=4•$\frac{b}{k}$，
又$\overrightarrow{OA}$$•\overrightarrow{OB}$=0，则x₁x₂+y₁y₂=0，
即$\frac{{b}^{2}}{{k}^{2}}$+4•$\frac{b}{k}$=0，
解得b=0（舍去）或b=-4k②，
故直线l的方程为：y=kx-4k=k（x-4），故直线过定点（4，0），
（2）当直线l斜率不存在时，设它的方程为x=m，显然m＞0，
联立方程解得y=±2$\sqrt{m}$，即y₁y₂=-4m
又因为$\overrightarrow{OA}$$•\overrightarrow{OB}$=0，所以可得x₁x₂+y₁y₂=0，即m²-4m=0，
解得m=0（舍去）或m=4
可知直线l方程为：x=4，
故直线过定点（4，0）．
设AB的方程为x=my+4，代入y²=4x，可得y²-4my-16=0，
∴y₁y₂=-16；
S_△ABO=$\frac{1}{2}$×4×（y₁-y₂），
S_△BOF=$\frac{1}{2}$×（-y₂），
∴S_△ABO-S_△BOF=2y₁-$\frac{3}{2}$y₂=2y₁+$\frac{24}{{y}_{1}}$≥2$\sqrt{2{y}_{1}×\frac{24}{{y}_{1}}}$=8$\sqrt{3}$．
故选：C．

点评 本题考查向量垂直的条件，同时考查直线与抛物线的位置关系，以及证明直线恒过定点，属于中档题．