设a,b为异面直线,EF为a,b的公垂线,α为过EF的中点且与a,b平行的平面,M为a上任一点,N为b上任一点,求证线段MN被平面α二等分.
【答案】
分析:过直线b作平面β∥α,过直线a及公垂线EF作一平面,在此平面内作MC∥EF,且与平面α,β分别交于B、C两点,设EF、MN分别与平面α交于点A、D,根据中位线可得D是MN的中点.
解答: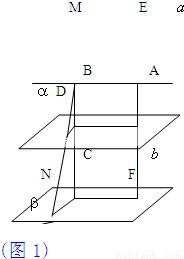
证明:过直线b作平面β∥α(如图1).
过直线a及公垂线EF作一平面,在此平面内作MC∥EF,且与平面α,β分别交于B、C两点,
设EF、MN分别与平面α交于点A、D,
∵点A是EF的中点,
又ME∥BA∥CF,
∴点B是MC的中点,
又∵DB∥NC,
∴D是MN的中点.
点评:本小题主要考查平面与平面平行的性质,以及平面的基本性质及推论,考查空间想象能力、运算能力和推理论证能力,属于基础题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案