A
分析：根据题意画出三角形AOB的内切圆，如图所示，由圆F与x轴和y轴都相切，设出圆F的半径为r，进而写出圆心F的坐标，根据直线AB与圆F相切，圆心到直线的距离d等于圆的半径r，利用点到直线的距离公式表示出d，让d等于r列出关于r的方程，求出方程的解即可得到半径r的值，进而得到圆心F的坐标，根据求出的圆心坐标和半径写出圆F的标准方程即为△AOB内切圆的方程．
解答：
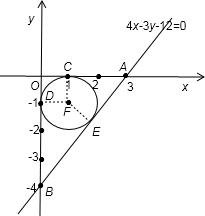
解：根据题意画出图形，如图所示：⊙F为△AOB的内切圆，
设⊙F的半径为r，所以圆心F的坐标为（r，-r），又⊙F与直线AB相切，
∴圆心F到直线的距离d=
=r，解得r=1或r=6（舍去），
∴圆心F的坐标为（1，-1），半径为1，
则△AOB内切圆的方程为（x-1）
2+（y+1）
2=1．
故选A
点评：此题考查学生掌握直线与圆相切时满足的关系，灵活运用点到直线的距离公式化简求值，会根据圆心和半径写出圆的标准方程，考查了数形结合的数学思想，是一道中档题．设出内切圆的半径表示出圆心F的坐标是解本题的关键．
