(Ⅰ)解:由已知得,

且2a+2c=4+4

,
解得a=2

,c=2,
又b
2=a
2-c
2=4,
所以椭圆G的方程为
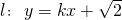
;
(Ⅱ)证明:由题意可知,直线l不过坐标原点,设A,B的坐标分别为(x
1,y
1),(x
2,y
2)(y
1>y
2),
(ⅰ)当直线l⊥x轴时,直线l的方程为x=m(m≠0)且-2

<m<2

,
则x
1=m,
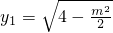
,x
2=m,
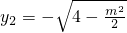
,
∵

,∴x
1x
2+y
1+y
2=0,
∴

,解得
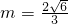
,
故直线l的方程为
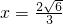
,
因此,点O(0,0)到直线l的距离为d=

,
又圆
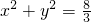
的圆心为O(0,0),半径r=

=d,
所以直线l与圆
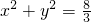
相切;
(ⅱ)当直线l不垂直于x轴时,设直线l的方程为y=kx+m,
由
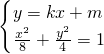
得(1+2k
2)x
2+4kmx+2m
2-8=0,
∴
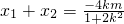
,
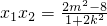
,
y
1y
2=(kx
1+m)(kx
2+m)=
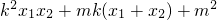
=
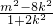
,
∵

,∴x
1x
2+y
1y
2=0,
故
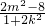
+
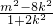
=0,即3m
2-8k
2-8=0,3m
2=8k
2+8,①
又圆
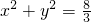
的圆心为O(0,0),半径r=

,
圆心O到直线l的距离为d=

,
∴
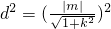
=
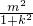
=
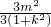
②,
将①式带入②式得
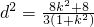
=

,
所以d=

=r,
因此,直线l与圆
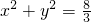
相切.
分析:(Ⅰ)由已知得,

且2a+2c=4+4

,联立方程组解出即得a,c,再由b
2=a
2-c
2求得b值;
(Ⅱ)由题意可知,直线l不过坐标原点,设A,B的坐标分别为(x
1,y
1),(x
2,y
2)(y
1>y
2),分情况讨论:(ⅰ)当直线l⊥x轴时,直线l的方程为x=m(m≠0)且-2

<m<2

,联立直线方程与椭圆方程易求A,B坐标,由

得x
1x
2+y
1+y
2=0,可求m,从而易判断直线与圆垂直;(ⅱ)当直线l不垂直于x轴时,设直线l的方程为y=kx+m,代入椭圆方程消掉y得x的二次方程,由韦达定理及x
1x
2+y
1+y
2=0可得k,m的方程①,根据点到直线的距离公式可表示圆心O到l的距离d,结合①式可求得d值,其恰好等于半径r;
点评:本题考查直线与圆锥曲线的位置关系、椭圆方程的求解,考查分类讨论思想,考查学生对问题的阅读理解能力及转化能力,弦长公式、点到直线距离公式、韦达定理是解决问题的基础知识,要熟练掌握.

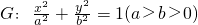 的离心率为
的离心率为 ,F1,F2为椭圆G的两个焦点,点P在椭圆G上,且△PF1F2的周长为
,F1,F2为椭圆G的两个焦点,点P在椭圆G上,且△PF1F2的周长为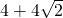 .
. (O为坐标原点),求证:直线l与圆
(O为坐标原点),求证:直线l与圆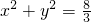 相切.
相切. 且2a+2c=4+4
且2a+2c=4+4 ,
, ,c=2,
,c=2,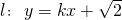 ;
; <m<2
<m<2 ,
,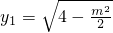 ,x2=m,
,x2=m,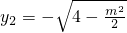 ,
, ,∴x1x2+y1+y2=0,
,∴x1x2+y1+y2=0, ,解得
,解得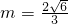 ,
,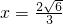 ,
, ,
,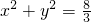 的圆心为O(0,0),半径r=
的圆心为O(0,0),半径r= =d,
=d,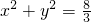 相切;
相切;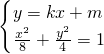 得(1+2k2)x2+4kmx+2m2-8=0,
得(1+2k2)x2+4kmx+2m2-8=0,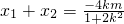 ,
,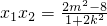 ,
,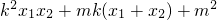 =
=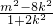 ,
, ,∴x1x2+y1y2=0,
,∴x1x2+y1y2=0,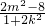 +
+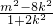 =0,即3m2-8k2-8=0,3m2=8k2+8,①
=0,即3m2-8k2-8=0,3m2=8k2+8,①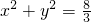 的圆心为O(0,0),半径r=
的圆心为O(0,0),半径r= ,
, ,
,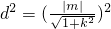 =
=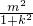 =
=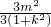 ②,
②,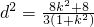 =
= ,
, =r,
=r,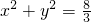 相切.
相切. 且2a+2c=4+4
且2a+2c=4+4 ,联立方程组解出即得a,c,再由b2=a2-c2求得b值;
,联立方程组解出即得a,c,再由b2=a2-c2求得b值; <m<2
<m<2 ,联立直线方程与椭圆方程易求A,B坐标,由
,联立直线方程与椭圆方程易求A,B坐标,由 得x1x2+y1+y2=0,可求m,从而易判断直线与圆垂直;(ⅱ)当直线l不垂直于x轴时,设直线l的方程为y=kx+m,代入椭圆方程消掉y得x的二次方程,由韦达定理及x1x2+y1+y2=0可得k,m的方程①,根据点到直线的距离公式可表示圆心O到l的距离d,结合①式可求得d值,其恰好等于半径r;
得x1x2+y1+y2=0,可求m,从而易判断直线与圆垂直;(ⅱ)当直线l不垂直于x轴时,设直线l的方程为y=kx+m,代入椭圆方程消掉y得x的二次方程,由韦达定理及x1x2+y1+y2=0可得k,m的方程①,根据点到直线的距离公式可表示圆心O到l的距离d,结合①式可求得d值,其恰好等于半径r;

 如图,在由圆O:x2+y2=1和椭圆C:
如图,在由圆O:x2+y2=1和椭圆C: 如图,A,B是椭圆C:
如图,A,B是椭圆C: