
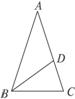
图1-3-5
思路分析:有一个角是36°的等腰三角形,它的底角是72°,而BD是底角的平分线,
∴∠CBD=36°,则可推出△ABC∽△BCD,进而由相似三角形的对应边成比例推出线段之间的比例关系.
证明:∵∠A=36°,AB=AC,∴∠ABC=∠C=72°.
又∵BD平分∠ABC,∴∠ABD=∠CBD=36°.
∴AD=BD=BC,且△ABC∽△BCD.∴BC∶AB=CD∶BC.
∴BC2=AB·CD.∴AD2=AC·CD.
深化升华 (1)有两个角对应相等,那么这两个三角形相似,这是判断两个三角形相似最常用的方法,并且根据相等的角的位置,可以确定哪些边是对应边.(2)要说明线段的乘积式ab=cd或平方式a2=bc,一般都是先证明比例式![]() 或
或![]() ,再根据比例的基本性质推出乘积式或平方式.
,再根据比例的基本性质推出乘积式或平方式.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案科目:高中数学 来源: 题型:

图1-3-15
(1)求证:△ABC∽△FCD;
(2)若S△FCD?=5,BC=10,求DE的长.
查看答案和解析>>
科目:高中数学 来源: 题型:

图1-3-6
(1)求证:△ABC∽△FCD;
(2)若S△FCD=5,BC=10,求DE的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
[2012·三明普通高中联考] 如图G8-5,已知四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠ABC=45°,DC=1,AB=2,PA⊥平面ABCD,PA=1.
(1)求证:AB∥平面PCD;
(2)求证:BC⊥平面PAC;
(3)若M是PC的中点,求三棱锥M-ACD的体积.
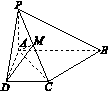
图G8-5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com