练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】甲、乙两艘轮船都要停靠在同一个泊位，它们可能在一昼夜的任意时刻到达．甲、乙两船停靠泊位的时间分别为4小时与2小时，求有一艘船停靠泊位时必需等待一段时间的概率．

    【答案】

    【解析】

    试题分析：分析知如两船到达的时间间隔超过了停泊的时间则不需要等待，要求一艘船停靠泊位时必须等待一段时间的概率即计算一船到达的时间恰好另一船还没有离开，此即是所研究的事件

    试题解析：甲比乙早到4小时内乙需等待，甲比乙晚到2小时内甲需等待．

    以x和y分别表示甲、乙两船到达泊位的时间，则有一

    艘船停靠泊位时需等待一段时间的充要条件为－2≤x－y≤4，在如

    图所示的平面直角坐标系内，(x，y)的所有可能结果是边长为24的

    正方形，而事件A“有一艘船停靠泊位时需等待一段时间”的可能结果由阴影部分表示．由几何概型公式得：

    P(A)＝＝.故有一艘船停靠泊位时必需等待一段时间的概率是.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    将圆上每一点的纵坐标保持不变，横坐标变为原来的2倍得到曲线．

    （1）写出曲线的参数方程；

    （2）以坐标原点为极点， 轴正半轴为极轴坐标建立极坐标系，已知直线的极坐标方程为，若分别为曲线和直线上的一点，求的最近距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】围建一个面积为360m2的矩形场地，要求矩形场地的一面利用旧墙（利用旧墙需维修，可供利用的旧墙足够长），其它三面围墙要新建，在旧墙的对面的新墙上要留一个宽度为2m的进出口，如图2所示，已知旧墙的维修费用为45元/m,新墙的造价为180元/m, 设利用旧墙的长度为（单位： ），修建此矩形场地围墙的总费用为（单位：元）.

    （Ⅰ）将表示为的函数；

    （Ⅱ）试确定,使修建此矩形场地围墙的总费用最小，并求出最小总费用。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某网络营销部门为了统计某市网友“双11”在某淘宝店的网购情况，随机抽查了该市当天60名网友的网购金额情况，得到如下数据统计表（如图）：

    若网购金额超过2千元的顾客定义为“网购达人”，网购金额不超过2千元的顾客定义为“非网购达人”，已知“非网购达人”与“网购达人”人数比恰好为3:2.

    （1）试确定的值，并补全频率分布直方图；

    （2）试营销部门为了进一步了解这60名网友的购物体验，从“非网购达人”、“网购达人”中用分层抽样的方法确定5人，若需从这5人中随机选取2人进行问卷调查，则恰好选取1名“网购达人”和1名“非网购达人”的概率是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

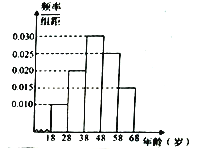
    【题目】某地为弘扬中国传统文化举办“传统文化常识问答活动”，随机对该市岁的人群抽取一个容量为的样本，并将样本数据分成五组： ，再将其按从左到右的顺序分别编号为第组，第组，…，第组，绘制了样本的频率分布直方图，并对回答问题情况进行统计后，结果如下表所示．

    组号

    分组

    回答正确的人数

    回答正确的人数占本组的比例

    　第组

    　

    　第组

    　

    　第组

    　

    　第组

    　

    　第组

    　

    ⑴分别求出, 的值；

    ⑵从组回答正确的人中用分层抽样的方法抽取人，则第组每组应各抽取多少人？

    ⑶在⑵的前提下，决定在所抽取的人中随机抽取人颁发幸运奖，求所抽取的人中第组至少有人获得幸运奖的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

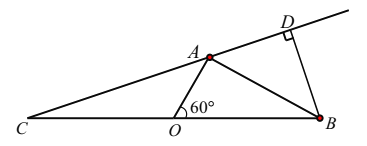
    【题目】随着节假日外出旅游人数增多，倡导文明旅游的同时，生活垃圾处理也面临新的挑战，某海滨城市沿海有三个旅游景点，在岸边两地的中点处设有一个垃圾回收站点（如图），两地相距10，从回收站观望地和地所成的视角为，且，设；

    （1）用分别表示和，并求出的取值范围；

    （2）某一时刻太阳与三点在同一直线，此时地到直线的距离为，求的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆与曲线有三个不同的交点.

    （1）求圆的方程；

    （2）已知点是轴上的动点， ， 分别切圆于， 两点.

    ①若，求及直线的方程；

    ②求证：直线恒过定点.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

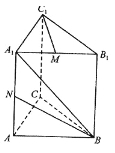
    【题目】如图，直三棱柱ABC-A1B1C1底面△ABC中，CA=CB=1，∠BCA=90°，棱AA1=2M，N分别是A1B1，A1A的中点。

    （1）求的长度；

    （2）求cos（，）的值；

    （3）求证：A1B⊥C1M。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆，过点作直线与椭圆交于两点．

    （1）若点平分线段，试求直线的方程；

    （2）设与满足（1）中条件的直线平行的直线与椭圆交于两点，与椭圆交于点，与椭圆交于点，求证：．

    查看答案和解析>>

    同步练习册答案