
如图,己知![]() 中,
中,![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 上的动点,且
上的动点,且![]() ,(
,(![]() )。
)。
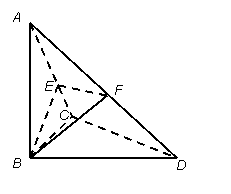
⑴求证:不论![]() 为何值,总有
为何值,总有![]() 平面
平面![]() ;
;
⑵若![]() ,求三棱锥
,求三棱锥![]() 的体积。
的体积。
 |
科目:高中数学 来源: 题型:
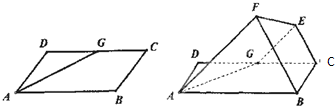 如图,己知平行四边形ABCD中,∠BAD=60°,AB=6,AD=3,G为CD中点,现将梯形ABCG沿着AG折起到AFEG.
如图,己知平行四边形ABCD中,∠BAD=60°,AB=6,AD=3,G为CD中点,现将梯形ABCG沿着AG折起到AFEG.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,己知平行四边形ABCD中,∠BAD=60°,AB=6,AD=3,G为CD中点,现将梯形ABCG沿着AG折起到AFEG.
如图,己知平行四边形ABCD中,∠BAD=60°,AB=6,AD=3,G为CD中点,现将梯形ABCG沿着AG折起到AFEG.| π | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
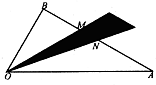 如图,己知|
如图,己知|| OA |
| OB |
| OP |
| OA |
| OB |
| A、①②④ | B、①③④ |
| C、①③⑤ | D、②⑤ |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省惠州市高三第三次调研考试数学文卷 题型:解答题
(本题满分14分)
如图,己知 中,
中,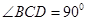 ,
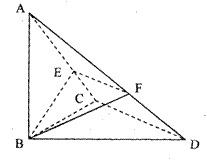
,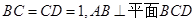 ,
, 且
且
(1)求证:不论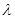 为何值,总有
为何值,总有
(2)若 求三棱锥
求三棱锥 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com