若x=3是函数f(x)=aln(1+x)+x2-10x的一个极值点.
(1)求函数f(x)的单调区间;
(2)若直线y=b与函数y=f(x)的图象有3个交点,求b的取值范围.
【答案】
分析:(1)因为
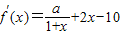
,所以
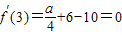
,因此a=16,由此能求出f(x)的单调区间.
(2)由(1)知,f(x)在(-1,1)内单调增加,在(1,3)内单调减少,在(3,+∞)上单调增加,故在f(x)的三个单调区间(-1,1),(1,3),(3,+∞),直线y=b与y=f(x)的图象各有一个交点,由此能求出b的取值范围.
解答:解:(1)因为
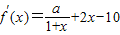
,
所以
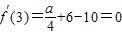
,因此a=16…2分
故 f(x)=16ln(1+x)+x
2-10x,x∈(-1,+∞),
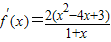
…4分
当x∈(-1,1)∪(3,+∞)时,f′(x)>0,
当x∈(1,3)时,f′(x)<0,
所以f(x)的单调增区间是(-1,1),(3,+∞),f(x)的单调减区间是(1,3)…6分
(2)由(1)知,f(x)在(-1,1)内单调增加,
在(1,3)内单调减少,在(3,+∞)上单调增加,
所以f(x)的极大值为f(1)=16ln2-9,极小值为f(3)=32ln2-21,…8分
所以在f(x)的三个单调区间(-1,1),(1,3),(3,+∞),
直线y=b与y=f(x)的图象各有一个交点,
当且仅当f(3)<b<f(1).
因此b的取值范围为(32ln2-21,16ln2-9).…12分.
点评:本题考查函数的单调性的求法,考查满足条件的实数的取值范围的求法.解题时要认真审题,仔细解答,注意等价转化思想的合理运用.

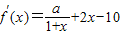 ,所以
,所以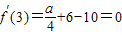 ,因此a=16,由此能求出f(x)的单调区间.
,因此a=16,由此能求出f(x)的单调区间.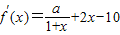 ,
,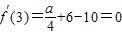 ,因此a=16…2分
,因此a=16…2分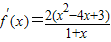 …4分
…4分

 名校通行证有效作业系列答案
名校通行证有效作业系列答案