
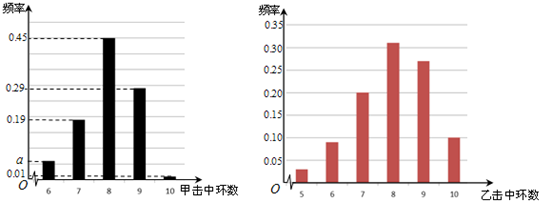
根据以往的成绩记录,甲、乙两名队员射击击中目标靶的环数的频率分布情况如图所示.
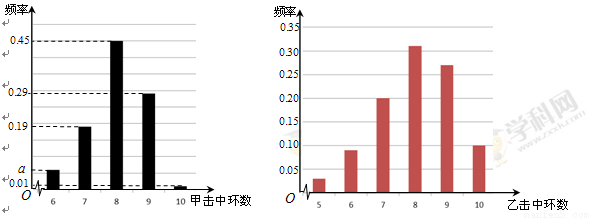
假设每名队员每次射击相互独立.
(Ⅰ)求上图中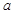 的值;
的值;
(Ⅱ)队员甲进行三次射击,求击中目标靶的环数不低于8环的次数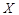 的分布列及数学期望(频率当作概率使用);
的分布列及数学期望(频率当作概率使用);
(Ⅲ)由上图判断,在甲、乙两名队员中,哪一名队员的射击成绩更稳定?(结论不需证明)
(Ⅰ)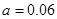 ;(Ⅱ)
;(Ⅱ)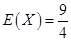 ;(Ⅲ)甲队员的射击成绩更稳定
;(Ⅲ)甲队员的射击成绩更稳定
【解析】
试题分析:(Ⅰ)由频率和为1可求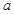 的值。(Ⅱ)从图中可以得到击中目标靶的环数不低于8环的概率,队员甲进行三次射击属于独立重复事件,符合二项分布。可根据独立重复事件概率公式
的值。(Ⅱ)从图中可以得到击中目标靶的环数不低于8环的概率,队员甲进行三次射击属于独立重复事件,符合二项分布。可根据独立重复事件概率公式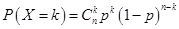 求其概率,再根据数学期望公式求其期望值,也可用二项分布列的数学期望公式求其期望值。(Ⅲ)甲队员的射击成绩较集中、波动较小,相对稳定。
求其概率,再根据数学期望公式求其期望值,也可用二项分布列的数学期望公式求其期望值。(Ⅲ)甲队员的射击成绩较集中、波动较小,相对稳定。
试题解析:解:(Ⅰ)由上图可得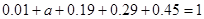 ,
,
所以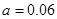 .
3分
.
3分
(Ⅱ)由图可得队员甲击中目标靶的环数不低于8环的概率为
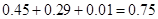 4分
4分
由题意可知随机变量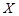 的取值为:0,1,2,3.
5分
的取值为:0,1,2,3.
5分
事件“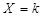 ”的含义是在3次射击中,恰有k次击中目标靶的环数不低于8环.
”的含义是在3次射击中,恰有k次击中目标靶的环数不低于8环.
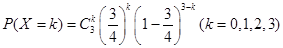
 8分
8分
即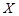 的分布列为
的分布列为
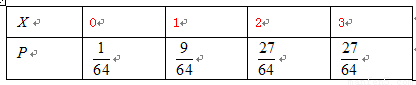
所以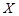 的期望是
的期望是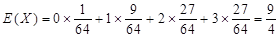 .
10分
.
10分
(Ⅲ)甲队员的射击成绩更稳定. 13分
考点:二项分布列、数学期望及方差的意义,考查数据处理能力、运算能力。


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
 根据以往的成绩记录,甲、乙两名队员射击击中目标靶的环数的频率分布情况如图所示:
根据以往的成绩记录,甲、乙两名队员射击击中目标靶的环数的频率分布情况如图所示:查看答案和解析>>
科目:高中数学 来源:2013-2014学年北京市海淀区高三上学期期末考试文科数学试卷(解析版) 题型:解答题
根据以往的成绩记录,甲、乙两名队员射击击中目标靶的环数的频率分布情况如图所示
(Ⅰ)求上图中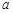 的值;
的值;
(Ⅱ)甲队员进行一次射击,求命中环数大于7环的概率(频率当作概率使用);
(Ⅲ)由上图判断甲、乙两名队员中,哪一名队员的射击成绩更稳定(结论不需证明).
查看答案和解析>>
科目:高中数学 来源:2013届度宁夏高二下学期期中考试理科数学试卷(解析版) 题型:解答题
12分)
要从两名同学中挑出一名,代表班级参加射击比赛,根据以往的成绩记录同学甲击中目标的环数为X1的分布列为
|
X1 |
5 |
6 |
7 |
8 |
9 |
10 |
|
P |
0.03 |
0.09 |
0.20 |
0.31 |
0.27 |
0.10 |
同学乙击目标的环数X2的分布列为
|
X2 |
5 |
6 |
7 |
8 |
9 |
|
P |
0.01 |
0.05 |
0.20 |
0.41 |
0.33 |
(1)请你评价两位同学的射击水平(用数据作依据);
(2)如果其它班参加选手成绩都在9环左右,本班应派哪一位选手参赛,如果其它班参赛选手的成绩都在7环左右呢?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com