
分析 ①设P(x0,y0),则${k}_{P{B}_{1}}•{k}_{P{B}_{2}}$=$\frac{{y}_{0}+b}{{x}_{0}}•\frac{{y}_{0}-b}{{x}_{0}}$=$\frac{{y}_{0}^{2}-{b}^{2}}{{x}_{0}^{2}}$,即可判断出正误;
②由于点P在圆x2+y2=b2外,可得${x}_{0}^{2}+{y}_{0}^{2}-{b}^{2}$>0,利用数量积运算性质可得:$\overrightarrow{P{B}_{1}}$•$\overrightarrow{P{B}_{2}}$=(-x0,-b-y0)•(-x0,b-y0)=${x}_{0}^{2}+{y}_{0}^{2}-{b}^{2}$,即可判断出正误;
③当点P在长轴的顶点上时,∠B1PB2最小且为锐角,设△PB1B2的外接圆半径为r,由正弦定理可得:2r=$\frac{2b}{sin∠{B}_{1}P{B}_{2}}$≤$\frac{2b}{sin∠{B}_{1}A{B}_{2}}$=$\frac{2b}{sin2∠OA{B}_{2}}$=$\frac{2b}{\frac{2ab}{{a}^{2}+{b}^{2}}}$=$\frac{{a}^{2}+{b}^{2}}{a}$,即可判断出正误;
④直线PB1的方程为:y+b=$\frac{{y}_{0}+b}{{x}_{0}}x$,直线QB2的方程为:$y-b=\frac{{y}_{0}-b}{-{x}_{0}}x$,两式相乘可得:y2-b2=$\frac{{y}_{0}^{2}-{b}^{2}}{-{x}_{0}^{2}}$x2,化为$\frac{{y}^{2}}{{b}^{2}}-\frac{{x}^{2}}{{a}^{2}}$=1,即可判断出正误.
解答 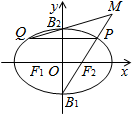 解:①设P(x0,y0),$\frac{{x}_{0}^{2}}{{a}^{2}}+\frac{{y}_{0}^{2}}{{b}^{2}}=1$,则${k}_{P{B}_{1}}•{k}_{P{B}_{2}}$=$\frac{{y}_{0}+b}{{x}_{0}}•\frac{{y}_{0}-b}{{x}_{0}}$=$\frac{{y}_{0}^{2}-{b}^{2}}{{x}_{0}^{2}}$=-$\frac{{b}^{2}}{{a}^{2}}$,因此不正确;
解:①设P(x0,y0),$\frac{{x}_{0}^{2}}{{a}^{2}}+\frac{{y}_{0}^{2}}{{b}^{2}}=1$,则${k}_{P{B}_{1}}•{k}_{P{B}_{2}}$=$\frac{{y}_{0}+b}{{x}_{0}}•\frac{{y}_{0}-b}{{x}_{0}}$=$\frac{{y}_{0}^{2}-{b}^{2}}{{x}_{0}^{2}}$=-$\frac{{b}^{2}}{{a}^{2}}$,因此不正确;
②∵点P在圆x2+y2=b2外,∴${x}_{0}^{2}+{y}_{0}^{2}-{b}^{2}$>0,∴$\overrightarrow{P{B}_{1}}$•$\overrightarrow{P{B}_{2}}$=(-x0,-b-y0)•(-x0,b-y0)=${x}_{0}^{2}+{y}_{0}^{2}-{b}^{2}$>0,正确;③当点P在长轴的顶点上时,∠B1PB2最小且为锐角,设△PB1B2的外接圆半径为r,由正弦定理可得:
2r=$\frac{2b}{sin∠{B}_{1}P{B}_{2}}$≤$\frac{2b}{sin∠{B}_{1}A{B}_{2}}$=$\frac{2b}{sin2∠OA{B}_{2}}$=$\frac{2b}{\frac{2ab}{{a}^{2}+{b}^{2}}}$=$\frac{{a}^{2}+{b}^{2}}{a}$.∴$r≤\frac{{a}^{2}+{b}^{2}}{2a}$,
∴③△PB1B2的外接圆半径的最大值为$\frac{{a}^{2}+{b}^{2}}{2a}$,正确;
④直线PB1的方程为:y+b=$\frac{{y}_{0}+b}{{x}_{0}}x$,直线QB2的方程为:$y-b=\frac{{y}_{0}-b}{-{x}_{0}}x$,两式相乘可得:y2-b2=$\frac{{y}_{0}^{2}-{b}^{2}}{-{x}_{0}^{2}}$x2,
化为$\frac{{y}^{2}}{{b}^{2}}-\frac{{x}^{2}}{{a}^{2}}$=1,由于点P不与B1,B2重合,∴M的轨迹为双曲线的一部分,∴④不正确.
故答案为:②③.
点评 本题综合考查了椭圆的标准方程及其性质、斜率计算公式、正弦定理、三角形外接圆半径、直线相交问题、双曲线的标准方程,考查了推理能力与计算能力,属于难题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
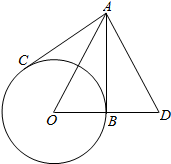 如图,AB,AC为⊙O的切线,B和C是切点,延长OB到D,使BD=OB,连接AD.如果∠DAC=78°,那么∠ADO等于( )
如图,AB,AC为⊙O的切线,B和C是切点,延长OB到D,使BD=OB,连接AD.如果∠DAC=78°,那么∠ADO等于( )| A. | 70° | B. | 64° | C. | 62° | D. | 51° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
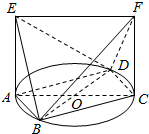 如图,已知AC,BD为圆O的任意两条直径,直线AE,CF是圆O所在平面的两条垂线,且线段AE=CF=$\sqrt{2}$,AC=2.
如图,已知AC,BD为圆O的任意两条直径,直线AE,CF是圆O所在平面的两条垂线,且线段AE=CF=$\sqrt{2}$,AC=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
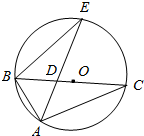 如图,△ABC内接于圆O,AE平分∠BAC交BC于点D,连接BE.
如图,△ABC内接于圆O,AE平分∠BAC交BC于点D,连接BE.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
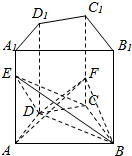 如图,在直四棱柱ABCD-A1B1C1D1中,点E,F分别在AA1,CC1上,且AE=$\frac{4}{5}$AA1,CF=$\frac{1}{3}$CC1,点A,C到BD的距离之比为2:3,则三棱锥E-BCD和F-ABD的体积比$\frac{{V}_{E-BCD}}{{V}_{F-ABD}}$=$\frac{18}{5}$.
如图,在直四棱柱ABCD-A1B1C1D1中,点E,F分别在AA1,CC1上,且AE=$\frac{4}{5}$AA1,CF=$\frac{1}{3}$CC1,点A,C到BD的距离之比为2:3,则三棱锥E-BCD和F-ABD的体积比$\frac{{V}_{E-BCD}}{{V}_{F-ABD}}$=$\frac{18}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
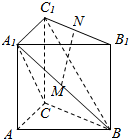 如图所示,在三棱柱ABC-A1B1C1中,∠ACB=90°,AA1⊥平面ABC,AC=BC=CC1,M,N分别为A1B,B1C1的中点.
如图所示,在三棱柱ABC-A1B1C1中,∠ACB=90°,AA1⊥平面ABC,AC=BC=CC1,M,N分别为A1B,B1C1的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com