
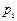 ,乙解决这个问题的概率是
,乙解决这个问题的概率是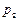 ,那么恰好有1人解决这个问题的概率是 ( )
,那么恰好有1人解决这个问题的概率是 ( )A.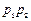 | B.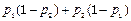 |
C.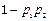 | D.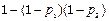 |
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:高中数学 来源:不详 题型:解答题
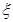 (单位:月)服从正态分布
(单位:月)服从正态分布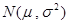 ,且使用寿命不少于
,且使用寿命不少于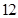 个月的概率为
个月的概率为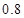 ,使用寿命不少于
,使用寿命不少于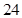 个月的概率为
个月的概率为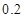 .
.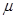 ;
;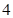 支这种新灯管,使用
支这种新灯管,使用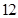 个月时进行一次检查,将已经损坏的灯管换下(中途不更换),求至少两支灯管需要更换的概率.
个月时进行一次检查,将已经损坏的灯管换下(中途不更换),求至少两支灯管需要更换的概率.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
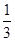 和
和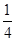 ,试求:
,试求:查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
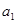 ,按下列方法操作一次产生一个新的实数:由甲、乙同时各抛一枚均匀的硬币,如果出现两个正面朝上或两个反面朝上,则把
,按下列方法操作一次产生一个新的实数:由甲、乙同时各抛一枚均匀的硬币,如果出现两个正面朝上或两个反面朝上,则把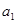 乘以2后再减去12;如果出现一个正面朝上,一个反面朝上,则把
乘以2后再减去12;如果出现一个正面朝上,一个反面朝上,则把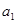 除以2后再加上12,这样就可得到一个新的实数
除以2后再加上12,这样就可得到一个新的实数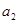 ,对
,对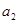 仍按上述方法进行一次操作,又得到一个新的实数
仍按上述方法进行一次操作,又得到一个新的实数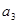 ,当
,当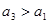 时,甲获胜,否则乙获胜。若甲获胜的概率为
时,甲获胜,否则乙获胜。若甲获胜的概率为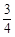 ,则
,则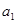 的取值范围是_________.
的取值范围是_________.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
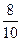 ,乙答题及格的概率为
,乙答题及格的概率为 ,丙答题及格的概率为
,丙答题及格的概率为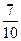 ,3人各答一次,则3人中只有1人答题及格的概率为 ( )
,3人各答一次,则3人中只有1人答题及格的概率为 ( ) (B)
(B)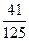 (C)
(C) 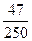 (D)以上全不对
(D)以上全不对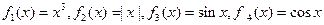 现从盒子中任取2张卡片,将卡片上的函数相乘得到一个新函数,所得函数为奇函数的概率是 ( )
现从盒子中任取2张卡片,将卡片上的函数相乘得到一个新函数,所得函数为奇函数的概率是 ( )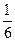 (B)
(B)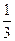 (C)
(C) (D)
(D)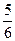
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com