等差数列﹛an﹜满足a4=20,a10=8
(I)求数列﹛an﹜的通项公式;
(II)求数列的前n项和Sn,指出当n为多少时Sn取最大值,并求出这个最大值.
解:(1)设公差等于d,∵a
4=20,a
10=8,∴a
10-a
4=8-20=6d,∴d=-2.
∴a
4=20=a
1+3d=a
1-6,∴a
1=26.
∴a
n=a
1+(n-1)d=26+(n-1)(-2)=28-2n.
(2)令a
n=28-2n=0,可得n=14,再由公差 d=-2<0可得,此数列为递减等差数列,第14项等于0,从第15项开始为负数,
故当n=13或14时S
n最大,最大值为
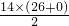
=182.
分析:(1)设公差等于d,由a
10-a
4=8-20=6d 求出d的值,再由等差数列的通项公式求出首项,从而得到数列﹛a
n﹜的通项公式.
(2)令a
n=0,可得n=14,再由公差 d=-2<0可得,此数列为递减等差数列,第14项等于0,从第15项开始为负数,故当n=13或14时S
n最大,利用等差数列的前n项和公式求出S
n最大值.
点评:本题主要考查等差数列的定义和性质,等差数列的通项公式,等差数列的前n项和公式的应用,求出首项和公差d的值,是解题的关键,属于基础题.

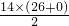 =182.
=182.

 备战中考寒假系列答案
备战中考寒假系列答案