
在图一所示的平面图形中, 是边长为
是边长为 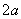 的等边三角形,
的等边三角形,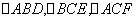 是分别以
是分别以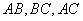 为底的全等的等腰三角形,现将该平面图形分别沿
为底的全等的等腰三角形,现将该平面图形分别沿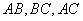 折叠,使
折叠,使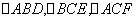 所在平面都与平面
所在平面都与平面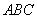 垂直,连接
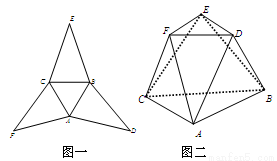
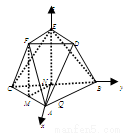
垂直,连接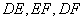 ,得到图二所示的几何体,据此几何体解决下面问题.
,得到图二所示的几何体,据此几何体解决下面问题.
(1)求证: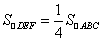 ;
;
(2)当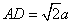 时,求三棱锥
时,求三棱锥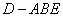 的体积
的体积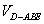 ;
;
(3)在(2)的前提下,求二面角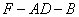 的余弦值.
的余弦值.
(1)通过计算体积证明。
(2)二面角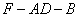 是钝二面角,
是钝二面角, .
.
【解析】
试题分析:(1)证明:如图,
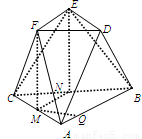
分别取AC、BC中点M、N,连接FM,EN,MN,
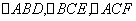 是全等的等腰三角形,
是全等的等腰三角形,
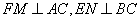 ,
,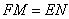 ,又
,又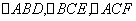 所在平面都与平面
所在平面都与平面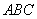 垂直,
垂直,
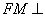 平面ABC,
平面ABC,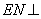 平面ABC,
平面ABC,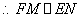 ,
, 四边形EFMN是平行四边形,
四边形EFMN是平行四边形,
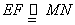 ,又
,又 ,
,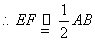 ,同理可得:
,同理可得: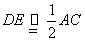 ,
,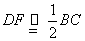 ,故
,故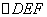 是边长为
是边长为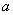 的正三角形,
的正三角形,
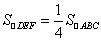 .···
.···
过M作MQ 于Q,解得MQ=
于Q,解得MQ=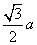 ,即为M到平面ABD的距离,由(1)可知平面MNEF
,即为M到平面ABD的距离,由(1)可知平面MNEF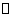 平面ABD,
平面ABD, E到平面ABD的距离为
E到平面ABD的距离为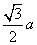 ,
,
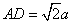 ,
,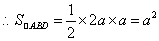
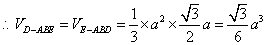 .···
.···
分别以NA、NB、NE所在直线为x、y、z轴建立空间直角坐标系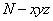 ,
,
依题意得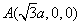 ,
,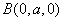 ,
,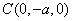 ,
, 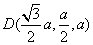 ,
,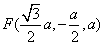 ,
,
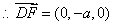 ,
,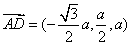 ,
,
设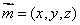 是平面ADF的一个法向量,
是平面ADF的一个法向量,
则有 ,即
,即 ,
,
令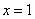 ,得
,得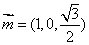 ,
,
又易知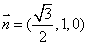 是平面ABD的一个法向量,
是平面ABD的一个法向量,
设二面角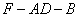 的平面角为
的平面角为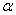 ,
,
有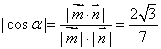 ,
,
又 二面角
二面角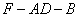 是钝二面角,
是钝二面角, .···(12分)
.···(12分)
考点:本题主要考查立体几何中的平行关系、垂直关系,体积计算、角的计算。
点评:中档题,立体几何题,是高考必考内容,往往涉及垂直关系、平行关系、角、距离、体积的计算。在计算问题中,有“几何法”和“向量法”。利用几何法,要遵循“一作、二证、三计算”的步骤。利用向量则能简化证明过程,对计算能力要求高。解答立体几何问题,另一个重要思想是“转化与化归思想”,即注意将空间问题转化成平面问题。


科目:高中数学 来源: 题型:
 (2012•盐城一模)在综合实践活动中,因制作一个工艺品的需要,某小组设计了如图所示的一个门(该图为轴对称图形),其中矩形ABCD的三边AB、BC、CD由长6分米的材料弯折而成,BC边的长为2t分米(1≤t≤
(2012•盐城一模)在综合实践活动中,因制作一个工艺品的需要,某小组设计了如图所示的一个门(该图为轴对称图形),其中矩形ABCD的三边AB、BC、CD由长6分米的材料弯折而成,BC边的长为2t分米(1≤t≤| 3 |
| 2 |
| 9 |
| 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示的一组图形为某一四棱锥S—ABCD的侧面与底面,
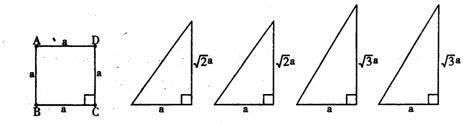
(1)指出各侧棱长;
(2)在(1)的条件下,过A且垂直于SC的平面分别交于SB、SC、SD于E、F、G.
求(1)(2)的条件下,求二面角A—SC—B的大小.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省南京市、盐城市高三第一次模拟考试数学(解析版) 题型:解答题
(本小题满分14分)
在综合实践活动中,因制作一个工艺品的需要,某小组设计了如图所示的一个门(该图为轴对
称图形),其中矩形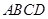 的三边
的三边 、
、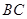 、
、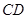 由长6分米的材料弯折而成,
由长6分米的材料弯折而成,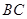 边的长
边的长
为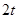 分米(
分米(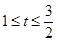 );曲线
);曲线 拟从以下两种曲线中选择一种:曲线
拟从以下两种曲线中选择一种:曲线 是一段余弦曲线
是一段余弦曲线
(在如图所示的平面直角坐标系中,其解析式为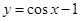 ),此时记门的最高点
),此时记门的最高点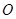 到
到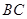
边的距离为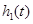 ;曲线
;曲线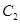 是一段抛物线,其焦点到准线的距离为
是一段抛物线,其焦点到准线的距离为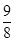 ,此时记门的最高点
,此时记门的最高点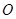
到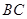 边的距离为
边的距离为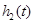 .
.
(1)试分别求出函数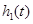 、
、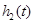 的表达式;
的表达式;
(2)要使得点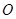 到
到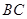 边的距离最大,应选用哪一种曲线?此时,最大值是多少?
边的距离最大,应选用哪一种曲线?此时,最大值是多少?

查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示的一组图形为某一四棱锥S―ABCD的侧面与底面;
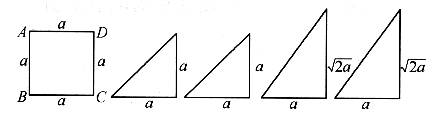
(1)请画出四棱锥S―ABCD的示意图,并判断是否存在一条侧棱垂直于底面?如果存在,请给出证明;
(2)若SA⊥平面ABCD,E为AB中点,求二面角E―SC―D的大小;
(3)在(2)的条件下,求点D到平面SEC的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com