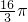A
分析:取AB中点E,连接PE、CE,可证出△PAE≌△PBE≌△PCE,得到∠CEP=90°即PE⊥CE,所以PE⊥平面ABC.因此,三棱锥P-ABC外接球的球心O在直线PE上,设PO=AO=R,建立关于R的方程并解之得R=

,最后结合球的表面积为公式,可得外接球的表面积.
解答:
取AB中点E,连接PE、CE
∵△ABC中,∠ACB=90°,E为AB中点
∴EA=EB=EC=

AB
又∵PA=PB=PC,PE公用,∴△PAE≌△PBE≌△PCE
∵△PAB中,PA=PB=2,EA=EB=1,∴PE⊥AB,PE=

可得∠AEP=∠BEP=∠CEP=90°,即得PE⊥CE,
∵AB、CE是平面ABC内的相交直线
∴PE⊥平面ABC
因此,三棱锥P-ABC外接球的球心O必在直线PE上,设PO=AO=R,得
OE
2+AE
2=OA
2,即(

-R)
2+1
2=R
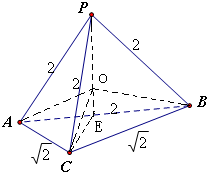
2,解之得R=

∴三棱锥P-ABC外接球的表面积为S=4πR
2=
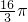
故选:A
点评:本题给出特殊的三棱锥,求它的外接球的表面积,着重考查了空间线面垂直的判定与性质和球的表面积公式等知识,属于中档题.

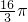

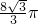
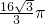
 ,最后结合球的表面积为公式,可得外接球的表面积.
,最后结合球的表面积为公式,可得外接球的表面积. 取AB中点E,连接PE、CE
取AB中点E,连接PE、CE AB
AB
 -R)2+12=R2,解之得R=
-R)2+12=R2,解之得R=