
为了解某校学生的视力情况,现采用随机抽样的方式从该校的A,B两班中各抽5名学生进行视力检测.检测的数据如下:
A班5名学生的视力检测结果:4.3,5.1,4.6,4.1,4.9.
B班5名学生的视力检测结果:5.1,4.9,4.0,4.0,4.5.
(1)分别计算两组数据的平均数,从计算结果看,哪个班的学生视力较好?;
(2)由数据判断哪个班的5名学生视力方差较大?(结论不要求证明)
(3)根据数据推断A班全班40名学生中有几名学生的视力大于4.6?
(1)A班学生的视力较好;(2)B班5名学生视力的方差较大;(3)A班有16名学生视力大于4.6.
解析试题分析:本题考查平均数、方差、随机事件的概率等基础知识,考查学生的分析问题解决问题的能力、计算能力.第一问,用所有视力的和除以5得到平均数,再比较大小,哪个班的平均数大哪个班的视力好;第二问,方差越小越稳定,利用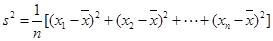 计算两个班的视力的方差比较大小;第三问,先得出5名学生视力大于4.6的频率,再估计全班40名学生的视力大于4.6的人数.
计算两个班的视力的方差比较大小;第三问,先得出5名学生视力大于4.6的频率,再估计全班40名学生的视力大于4.6的人数.
试题解析:(1)A班5名学生的视力平均数为 ,
,
B班5名学生的视力平均数为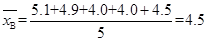 .
.
从数据结果来看A班学生的视力较好
(2)B班5名学生视力的方差较大
(3)在A班抽取的5名学生中,视力大于4.6的有2名,
所以这5名学生视力大于4.6的频率为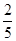 .
.
所以全班40名学生中视力大于4.6的大约有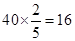 名,
名,
则根据数据可推断A班有16名学生视力大于4.6.
考点:平均数、方差、随机事件的概率.


科目:高中数学 来源: 题型:解答题
红队队员甲、乙与蓝队队员A、B进行围棋比赛,甲对A、乙对B各比一盘.已知甲胜A,乙胜B的概率分别为0.6、0.5.假设各盘比赛结果相互独立.
(1)求红队至少一名队员获胜的概率;
(2)用ξ表示红队队员获胜的总盘数,求ξ的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设有关于x的一元二次方程x2+2ax+b2="0." (l)若a是从0,1,2,3四个数中任取的一个数,b是从0,1,2三个数中任取的一个数,求方程有实根的概率;(2)若a是从区间[0,t+1]任取的一个数,b是从区间[0,t]任取的一个数,其中t满足2≤t≤3,求方程有实根的概率,并求出其概率的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一个袋中装有8个大小质地相同的球,其中4个红球、4个白球,现从中任意取出四个球,设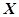 为取得红球的个数.
为取得红球的个数.
(1)求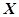 的分布列;
的分布列;
(2)若摸出4个都是红球记5分,摸出3个红球记4分,否则记2分.求得分的期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下列表:
| | 喜爱打篮球 | 不喜爱打篮球 | 合计 |
| 男生 | | 5 | |
| 女生 | 10 | | |
| 合计 | | | 50 |
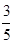 .
.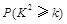 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
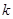 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
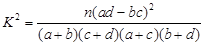 ,其中
,其中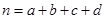 )
)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某射手进行射击训练,假设每次射击击中目标的概率为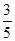 ,且每次射击的结果互不影响,已知射手射击了5
,且每次射击的结果互不影响,已知射手射击了5
次,求:
(1)其中只在第一、三、五次击中目标的概率;
(2)其中恰有3次击中目标的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
假设某班级教室共有4扇窗户,在每天上午第三节课上课预备铃声响起时,每扇窗户或被敞开或被关闭,且概率均为0.5.记此时教室里敞开的窗户个数为X.
(1)求X的分布列;
(2)若此时教室里有两扇或两扇以上的窗户被关闭,班长就会将关闭的窗户全部敞开,否则维持原状不变.记每天上午第三节课上课时该教室里敞开的窗户个数为Y,求Y的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售.如果当天卖不完,剩下的玫瑰花作垃圾处理.
(1)若花店一天购进17枝玫瑰花,求当天的利润y(单位:元)关于当天需求量n(单位:枝,n∈N)的函数解析式;
(2)花店记录了100天玫瑰花的日需求量(单位:枝),整理得下表:
| 日需求量n | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 频数 | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(13分)(2011•陕西)如图,A地到火车站共有两条路径L1和L2,现随机抽取100位从A地到火车站的人进行调查,调查结果如下:
| 所用时间(分钟) | 10~20 | 20~30 | 30~40 | 40~50 | 50~60 |
| 选择L1的人数 | 6 | 12 | 18 | 12 | 12 |
| 选择L2的人数 | 0 | 4 | 16 | 16 | 4 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com