若Sn是等差数列{an}的前n项和,其首项a1>0,a99+a100>0,a99•a100<0,则使Sn>0成立的最大自然数n是( )
A.198
B.199
C.200
D.201
【答案】
分析:先根据a
99•a
100<0,a
1>0,a
99+a
100>0,判断出a
100<0,利用等差数列通项公式可知a
1+99d<0同乘以2得2a
1+199d<0,即a
99+a
101<0,根据a
99+a
100>0,可知在连续相邻的两项中,a
99+a
100>0之后的和都将小于0.要使S
n>0成立,取最大自然数,n满足 a
99+a
100=a
1+a
198,进而根据等差数列求和公式求得答案.
解答:解:∵a
99•a
100<0,
∴a
99和a
100异号
∵a
1>0,a
99+a
100>0,
∴a
99>0,a
100<0,即a
1+99d<0
∴2a
1+199d<0,即a
99+a
101<0,a
100+a
101<0
∵a
99+a
100>0,
∴在连续相邻的两项中,a
99+a
100>0之后的和都将小于0.
要使S
n>0成立,取最大自然数,n满足
a
99+a
100=a
1+a
198,此时S
n=
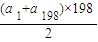
>0
∴n=198
故选A
点评:本题主要考查了等差数列的性质.考查了学生的推理能力和运算能力.

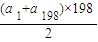 >0
>0
