
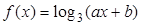 的图象经过点
的图象经过点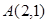 和
和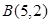 ,记
,记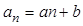 (
(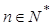 )
)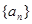 的通项公式;
的通项公式;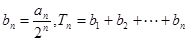 ,若
,若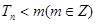 ,求
,求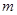 的最小值;
的最小值;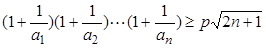 对一切
对一切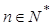 均成立的最大实数
均成立的最大实数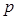 .
.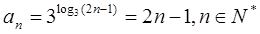 ;
;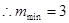 ; (3)
; (3) .
. 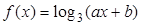 的图象经过点
的图象经过点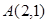 和
和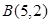 ,记
,记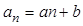 ,联立方程组得到a,b的值。
,联立方程组得到a,b的值。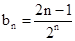 ,然后利用错位相减法得到数列的和。
,然后利用错位相减法得到数列的和。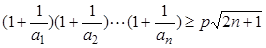 对一切
对一切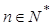 均成立,则可以分离参数p,得到关于n的表达式,进而求解数列的最值,得到参数p的范围。
均成立,则可以分离参数p,得到关于n的表达式,进而求解数列的最值,得到参数p的范围。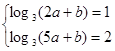 ,解得
,解得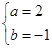 , …………2分
, …………2分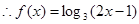
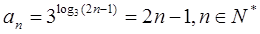 …………4分
…………4分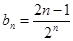 ,
, 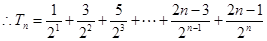 ①
①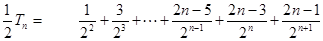 ② ①-②得
② ①-②得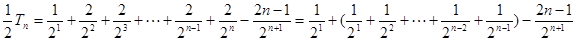
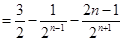 .
. 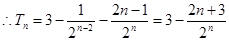 , …………7分
, …………7分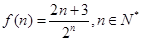 ,则由
,则由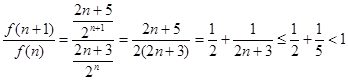
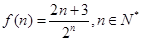 随
随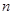 的增大而减小,
的增大而减小,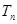 随
随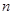 的增大而增大。
的增大而增大。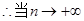 时,
时,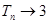
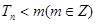 恒成立,
恒成立,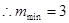 ………10分
………10分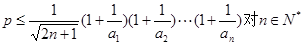 恒成立
恒成立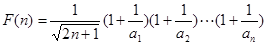 ,则
,则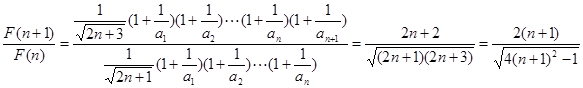
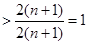 …………12分
…………12分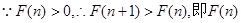 是随
是随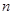 的增大而增大
的增大而增大 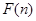 的最小值为
的最小值为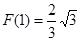 ,
,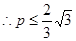 ,即
,即 . …………14分
. …………14分

 全程金卷系列答案
全程金卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com