函数f(x)=|lgx|+x-3的零点个数是________.
2
分析:先求出函数的定义域,再把函数转化为对应的方程,在坐标系中画出两个函数y
1=|lgx|,y
2=3-x(x>0)的图象求出方程的根的个数,即为函数零点的个数
解答:
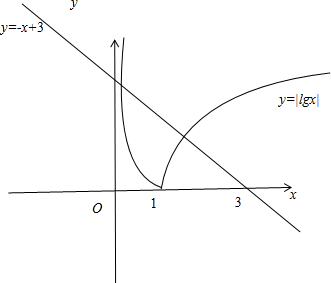
解:由题意,函数f(x)的定义域为(0,+∞)
由函数零点的定义,f(x)在(0,+∞)内的零点即是方程|lgx|=-x+3的根.
令y
1=|lgx|,y
2=-x+3(x>0),在一个坐标系中画出两个函数的图象:
由图得,两个函数图象有两个交点,
故方程有两个根,即对应函数有两个零点.
故答案为:2
点评:本题考查了函数零点、对应方程的根和函数图象之间的关系,通过转化和作图求出函数零点的个数
