
已知向量![]() ,
,![]() ,且当
,且当![]() 时,有
时,有![]() ; 当
; 当![]() 时,
时,![]() ∥
∥![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)求函数![]() 的单调递减区间;
的单调递减区间;
(3)若对![]() ,都有
,都有![]() ,求实数
,求实数![]() 的最小值.
的最小值.
解:(1)f(x)=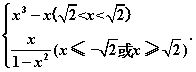 ……………………5分
……………………5分
(2)当|x|<![]() 时,由y′=3x2-1<0,解得-
时,由y′=3x2-1<0,解得-![]() <x<
<x<![]() ,
,
当|x|≥![]() 时,y′=
时,y′=![]() =
=![]() >0,
>0,
∴函数f(x)的单调递减区间为(-![]() ,
,![]() ). …………………10分
). …………………10分
(3)对x∈(-∞,-![]() ]∪[
]∪[![]() ,+∞),都有f(x)≤m,即m≥
,+∞),都有f(x)≤m,即m≥![]() ,
,
由(2)知当|x|≥![]() 时,y′=
时,y′=![]() >0,
>0,
∴函数f(x)在(-∞,-![]() ]和[
]和[![]() ,+∞)上都单调递增,
,+∞)上都单调递增,
f(-![]() )=
)=![]() =
=![]() ,f(
,f(![]() )=
)=![]() =-
=-![]() ,
,
当x≤-![]() 时,y=
时,y=![]() >0,∴0<f(x)≤f(-
>0,∴0<f(x)≤f(-![]() )=
)=![]() ,
,
同理可得,当x≥![]() 时,有-
时,有-![]() ≤f(x)<0,
≤f(x)<0,
综上所述,对x∈(-∞,-![]() ]∪[
]∪[![]() ,+∞),f(x)取得最大值
,+∞),f(x)取得最大值![]() ,
,
∴实数m的最小值为![]() . ………………………………15分
. ………………………………15分


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2009-2010学年北京市通州区高一(上)期末数学试卷(解析版) 题型:解答题
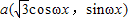 ,b(sinωx,0),且ω>0,设函数f(x)=(a+b)•b+k.
,b(sinωx,0),且ω>0,设函数f(x)=(a+b)•b+k. ,求ω的取值范围.
,求ω的取值范围.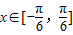 时,f(x)的最大值是2,求就k的值.
时,f(x)的最大值是2,求就k的值.查看答案和解析>>
科目:高中数学 来源:2011-2012学年重庆市高三第五次月考理科数学 题型:解答题
已知向量 ,
, ,定义
,定义 .
.
(1) 求出 的解析式.当
的解析式.当 时,它可以表示一个振动量,请指出其振幅,相位及初相.
时,它可以表示一个振动量,请指出其振幅,相位及初相.
(2)
 的图像可由
的图像可由 的图像怎样变化得到?
的图像怎样变化得到?
(3) 若 且
且 为△ABC的一个内角,求
为△ABC的一个内角,求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年辽宁省高三第二次阶段测试文科数学卷 题型:解答题
(本小题满分12分)已知向量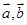 满足
满足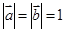 ,且
,且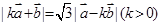 ,令
,令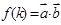 ,
,
(1)求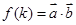 (用
(用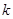 表示);
表示);
(2)当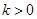 时,
时,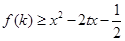 对任意的
对任意的 恒成立,求实数
恒成立,求实数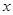 取值范围.
取值范围.
查看答案和解析>>
科目:高中数学 来源:2014届江西省高一第一次月考数学 题型:解答题
(12分) 已知函数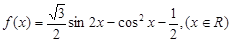
(1)当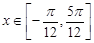 时,求函数
时,求函数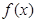 的最大值;(2)设
的最大值;(2)设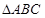 的内角
的内角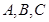 的对应边分别为
的对应边分别为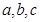 ,且
,且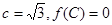 ,若向量
,若向量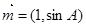 与向量
与向量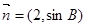 共线,求
共线,求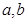 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com