
(满分12分)设底面边长为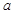 的正四棱柱
的正四棱柱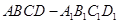 中,
中,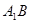 与平面
与平面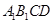 所成角为
所成角为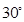 ;点
;点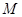 是棱
是棱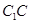 上一点.
上一点.

(1)求证:正四棱柱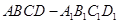 是正方体;
是正方体;
(2)若点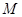 在棱
在棱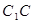 上滑动,求点
上滑动,求点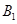 到平面
到平面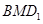 距离的最大值;
距离的最大值;
(3)在(2)的条件下,求二面角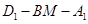 的大小.
的大小.
(1).证明:见解析;(2)点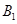 到平面
到平面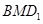 的最大距离是
的最大距离是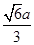 ;(3)
;(3)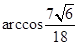 .
.
【解析】本试题主要考查了立体几何中正方体概念,和点到面的距离的最值和二面角的求解和运算的综合试题。
(1)利用正四棱柱的性质,加上题目中的边的关系,结合概念得到。
(2)对于点到面的距离关键是找到平面的垂线,利用面面垂直的性质定理得到点到面的距离的表示,从而求解最值。
(3)建立合理的空间直角坐标系,然后设出法向量来表示二面角的平面角的大小来解决。
(1).证明:设正四棱柱的侧棱长为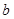 ,作
,作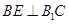 与
与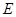 ,连接
,连接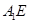 ,
,
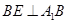 ,
,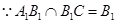 ,
, ,
,
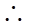
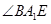 是
是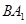 与
与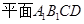 所成的角,
所成的角,
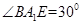
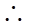
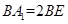 ,即
,即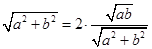
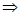
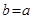
所以四棱柱正四棱柱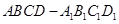 是正方体;......................4'
是正方体;......................4'
(2).设点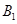 到平面
到平面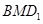 的距离为
的距离为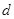 ,
,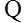
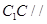 平面
平面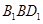 ,
, 点
点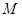 、
、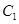 到平面
到平面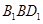 的距离相等为
的距离相等为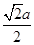 .在四面体
.在四面体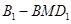 中,体积
中,体积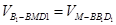 ,
,
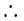
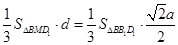
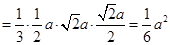
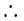
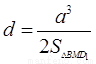 ,设
,设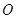 是
是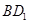 中点,当
中点,当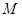 也是棱
也是棱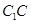 中点时,
中点时,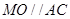 ,有
,有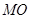
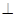 平面
平面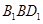 ,
,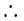
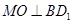 于
于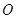 ,
,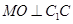 于
于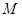 ,
,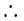
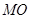 是一面直线
是一面直线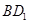 和
和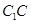 的公垂线段,
的公垂线段,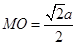 是
是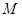 到直线
到直线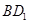 的最短距离,
的最短距离,
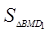 的最小值是
的最小值是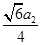
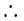
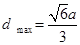 ,即点
,即点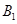 到平面
到平面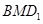 的最大距离是
的最大距离是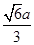 .....................8'
.....................8'
(3).以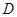 为原点,
为原点,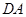 、
、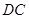 、
、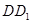 分别为
分别为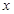 、
、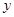 、
、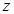 轴建立平面直角坐标系,由(2)知
轴建立平面直角坐标系,由(2)知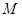 也是棱
也是棱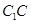 中点,则
中点,则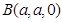 、
、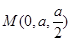 、
、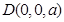 、
、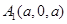 ,设平面
,设平面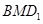 的法向量
的法向量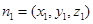 ,平面
,平面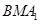 的法向量
的法向量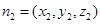 由
由
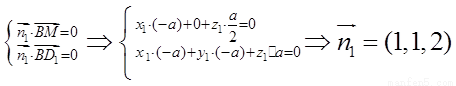 ;
;
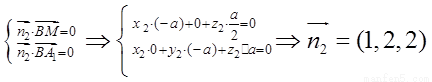 。
。
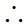
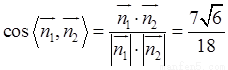
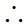 面角
面角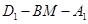 的大小是
的大小是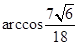 .............................12'
.............................12'


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:高中数学 来源: 题型:
()(本小题满分12分)如图,已知平面![]() 平行于三棱锥
平行于三棱锥![]() 的底面,等边三角形
的底面,等边三角形![]() 所在平面与面
所在平面与面![]() 垂直,且
垂直,且![]() ,设
,设![]() 。
。
(Ⅰ)证明:![]() 为异面直线
为异面直线![]() 与
与![]() 的公垂线;
的公垂线;
(Ⅱ)求点![]() 与平面
与平面![]() 的距离;
的距离;
(Ⅲ)求二面角![]() 的大小。
的大小。
查看答案和解析>>
科目:高中数学 来源:2010-2011学年河北省高三一轮检测复习数学理卷 题型:解答题
(本小题满分12分)
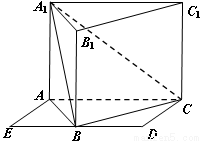
如图,侧棱垂直底面的三棱柱 的底面
的底面 位于平行四边形
位于平行四边形 中,
中,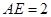 ,
,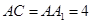 ,
,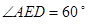 ,点
,点 为
为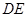 中点。
中点。
(Ⅰ)求证:平面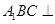 平面
平面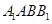 ;
;
(Ⅱ)设二面角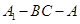 的大小为
的大小为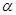 ,直线
,直线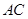 与
与
平面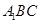 所成的角为
所成的角为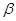 ,求
,求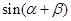 的值。
的值。
查看答案和解析>>
科目:高中数学 来源:2010-2011学年广西省高三高考模拟考试理数 题型:解答题
(本小题满分12分)(注意:在试题卷上作答无效)
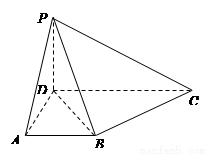
在四棱锥 中,侧面
中,侧面
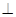 底面
底面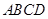 ,
,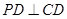 ,底面
,底面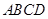 是直角梯形,
是直角梯形,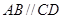 ,
,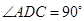 ,
,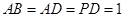 ,
,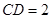 .
.
(Ⅰ)求证: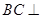 平面
平面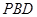 ;
;
(Ⅱ)设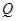 为侧棱
为侧棱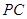 上一点,
上一点,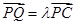 ,
,
试确定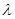 的值,使得二面角
的值,使得二面角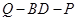 为
为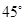 .
.
查看答案和解析>>
科目:高中数学 来源:2010-2011年四川省成都市高二3月月考数学试卷 题型:填空题
(本小题满分12分)
已知平行六面体中 ,
,
各条棱长均为 ,底面是正方形,且
,底面是正方形,且 ,
,
设 ,
, ,
, ,
,
(1)用 、
、 、
、 表示
表示 及求
及求 ;
;
(2)求异面直线 与
与 所成的角的余弦值。
所成的角的余弦值。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com