
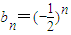 ��n��N*���ж�{an}��{bn}�Ƿ�Ϊ��p-�ڶ����С�����˵�����ɣ�
��n��N*���ж�{an}��{bn}�Ƿ�Ϊ��p-�ڶ����С�����˵�����ɣ� ��c1=1������p��ֵ��
��c1=1������p��ֵ�� ������n���������ԣ�p��ȡֵΪ0��
������n���������ԣ�p��ȡֵΪ0��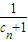 ��c1=1�����c2��ɶ϶�����p�ij�����Χ�����ɣ�xn+1-p����xn-p����0������������n�������ó����е������С��p��ż�������p�������������p��ż���С��p��Ȼ�����á����С��İ취����p��ֵ��
��c1=1�����c2��ɶ϶�����p�ij�����Χ�����ɣ�xn+1-p����xn-p����0������������n�������ó����е������С��p��ż�������p�������������p��ż���С��p��Ȼ�����á����С��İ취����p��ֵ��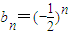 ������
������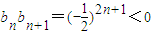 ������n����������p=0��
������n����������p=0��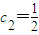 ��
��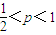 ��ʹ������������n�����У�cn+1-p����cn-p����0������
��ʹ������������n�����У�cn+1-p����cn-p����0������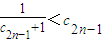 �����
�����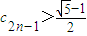 ��
��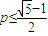 ��
��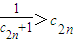 �����
�����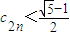 ����
����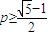 ��
�� ��
��
 ��
��
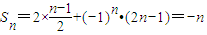
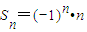 ��
��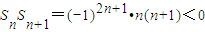 ������
������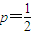 ʱ��
ʱ��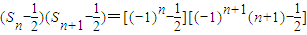
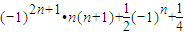
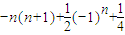 ��
��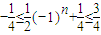 ��-n��n+1����-2��
��-n��n+1����-2��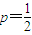 ��ʹ
��ʹ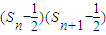 ��0������
��0������


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
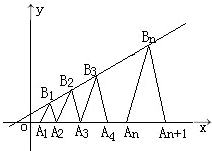 ����y=f��x���Ƕ�����R�ϵ�ż��������f��-1+x��=f��-1-x������x��[-2��-1]ʱ��f��x��=t��x+2��3-t��x+2����t��R�����Ǻ���y=f��x����ͼ���ڣ�
����y=f��x���Ƕ�����R�ϵ�ż��������f��-1+x��=f��-1-x������x��[-2��-1]ʱ��f��x��=t��x+2��3-t��x+2����t��R�����Ǻ���y=f��x����ͼ���ڣ�| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| n | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 �����⺯��f��x����x��D���ɰ���ͼ����һ�����з��������������з�������������{xn}��
�����⺯��f��x����x��D���ɰ���ͼ����һ�����з��������������з�������������{xn}��| 4x-2 |
| x+1 |
| 49 |
| 65 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
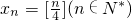 ����x1+x2+��+x4n=________��
����x1+x2+��+x4n=________���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2009-2010ѧ�걱���г�������һ���£���ĩ��ѧ�Ծ��������棩 ���ͣ������
 ����x1+x2+��+x4n= ��
����x1+x2+��+x4n= ���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com