
| x1+x2 | 2 |
| 9-1 |
| 3-1 |
| y2-y1 |
| x2-x1 |
| lnx2-lnx1 |
| x2-x1 |
| x1+x2 |
| 2 |
| x1+x2 |
| 2 |
| 2 |
| x1+x2 |
| lnx 2-lnx1 |
| x2-x1 |
| 2 |
| x1+x2 |
| x2 |
| x1 |
| 2(x2-x1) |
| x1+x2 |
2(
| ||
|
| x2 |
| x1 |
| 2(t-1) |
| t+1 |
| 4 |
| t+1 |
| 4 |
| t+1 |
| (t-1) 2 |
| t(t+1) 2 |
| 4 |
| t+1 |


科目:高中数学 来源: 题型:
| 1 |
| 2 |
| x1+x2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分15分)已知函数![]()
![]() 且导数
且导数![]() .
.
(Ⅰ)试用含有![]() 的式子表示
的式子表示![]() ,并求
,并求![]() 单调区间; (II)对于函数图象上的不同两点
单调区间; (II)对于函数图象上的不同两点![]() ,如果在函数图象上存在点
,如果在函数图象上存在点![]() (其中
(其中![]() )使得点
)使得点![]() 处的切线
处的切线![]() ,则称
,则称![]() 存在“伴侣切线”.特别地,当
存在“伴侣切线”.特别地,当![]() 时,又称
时,又称![]() 存在“中值伴侣切线”.试问:在函数
存在“中值伴侣切线”.试问:在函数![]() 上是否存在两点
上是否存在两点![]() 、
、![]() 使得它存在“中值伴侣切线”,若存在,求出
使得它存在“中值伴侣切线”,若存在,求出![]() 、
、![]() 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数![]() (
(![]() ),且
),且![]() .
.
(Ⅰ)试用含有![]() 的式子表示
的式子表示![]() ,并求
,并求![]() 的极值;
的极值;
(Ⅱ)对于函数![]() 图象上的不同两点
图象上的不同两点![]() ,
,![]() ,如果在函数图象上存在点
,如果在函数图象上存在点![]() (其中
(其中![]() ),使得点
),使得点![]() 处的切线
处的切线![]() ,则称
,则称![]() 存在“伴随切线”. 特别地,当
存在“伴随切线”. 特别地,当![]() 时,又称
时,又称![]() 存在“中值伴随切线”. 试问:在函数
存在“中值伴随切线”. 试问:在函数![]() 的图象上是否存在两点
的图象上是否存在两点![]() 、
、![]() 使得它存在“中值伴随切线”,若存在,求出
使得它存在“中值伴随切线”,若存在,求出![]() 、
、![]() 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年湖南省长沙市高三第三次月考文科数学卷 题型:解答题
已知函数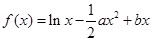 (
(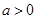 ),且
),且 .
.
(Ⅰ)试用含有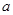 的式子表示
的式子表示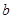 ,并求
,并求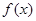 的极值;
的极值;
(Ⅱ)对于函数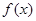 图象上的不同两点
图象上的不同两点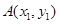 ,
,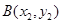 ,如果在函数图象上
,如果在函数图象上 存在点
存在点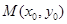 (其中
(其中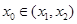 ),使得点
),使得点 处的切线
处的切线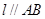 ,则称
,则称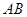 存在“伴随切线”. 特别地,当
存在“伴随切线”. 特别地,当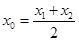 时,又称
时,又称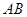 存在“中值伴随切线”. 试问:在函数
存在“中值伴随切线”. 试问:在函数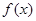 的图象上是否存在两点
的图象上是否存在两点 、
、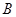 使得它存在“中值伴随切线”,若存在,求出
使得它存在“中值伴随切线”,若存在,求出 、
、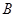 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com