
【题目】已知函数![]() ,其中
,其中 ![]() ,
,![]() 为自然对数的底数.
为自然对数的底数.
(Ⅰ)讨论函数![]() 的单调性;
的单调性;
(Ⅱ)当![]() 时,若函数
时,若函数![]() 的图象恒在直线
的图象恒在直线![]() 的上方,求实数a的取值范围.
的上方,求实数a的取值范围.
【答案】(Ⅰ)见详解;(Ⅱ)![]()
【解析】
(Ⅰ)由![]() 求导可得:
求导可得:![]() ,因为
,因为![]() 由
由![]() 可得
可得![]() ,再根据两者的大小关系进行分类讨论可得函数
,再根据两者的大小关系进行分类讨论可得函数![]() 的单调区间;
的单调区间;
(Ⅱ)由已知可得![]() 在
在![]() 上恒成立,再分类讨论
上恒成立,再分类讨论![]() 时,
时,![]() 时和
时和![]() 时函数
时函数![]() 的最小值,由
的最小值,由![]() 即可求解.
即可求解.
(Ⅰ)由![]() 求导可得:
求导可得:
![]()
![]()
![]() .
.
由![]() 可得
可得![]() ,且
,且![]() ,
,
①当![]() 时,即
时,即![]() ,
,
当![]() 或
或![]() 时
时![]() ,
,![]() 在此区间单调递增;
在此区间单调递增;
当![]() 时
时![]() ,
,![]() 在此区间单调递减;
在此区间单调递减;
②当![]() 时,即
时,即![]() ,
,
当![]() 或
或![]() 时
时![]() ,
,![]() 在此区间单调递增;
在此区间单调递增;
当![]() 时
时![]() ,
,![]() 在此区间单调递减;
在此区间单调递减;
③当![]() 时,即
时,即![]() ,
,
![]() ,
,![]() 在R上单调递增;
在R上单调递增;
(Ⅱ)由已知可得![]() 在
在![]() 上恒成立.
上恒成立.
①当![]() 时,由(Ⅰ)可知
时,由(Ⅰ)可知![]() 在
在![]() 上单调递增,
上单调递增,
![]() ,
,
![]() ,解得:
,解得:![]() ,
,
![]() ;
;
②当![]() 时,即
时,即![]()
由(Ⅰ)可知![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
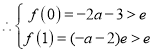 ,
,
解得![]() ,
,![]() ;
;
③当![]() 时,即
时,即![]() ,
,
由(Ⅰ)可知![]() 在
在![]() 上单调递减,
上单调递减,
![]() ,
,
![]() ,解得
,解得![]() ,
,![]() 此种情况a无解.
此种情况a无解.
综上,a的取值范围是![]()


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,![]() ,
,![]() 是经过小城
是经过小城![]() 的东西方向与南北方向的两条公路,小城
的东西方向与南北方向的两条公路,小城![]() 位于小城
位于小城![]() 的东北方向,直线距离
的东北方向,直线距离![]() .现规划经过小城
.现规划经过小城![]() 修建公路
修建公路![]() (
(![]() ,
,![]() 分别在
分别在![]() 与
与![]() 上),与
上),与![]() ,
,![]() 围成三角形区域
围成三角形区域![]() .
.
(1)设![]() ,
,![]() ,求三角形区域
,求三角形区域![]() 周长的函数解析式
周长的函数解析式![]() ;
;
(2)现计划开发周长最短的三角形区域![]() ,求该开发区域的面积.
,求该开发区域的面积.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在区间
在区间![]() 上有最小值1,最大值9.
上有最小值1,最大值9.
(1)求实数a,b的值;
(2)设![]() ,若不等式
,若不等式![]() 在区间
在区间![]() 上恒成立,求实数k的取值范围;
上恒成立,求实数k的取值范围;
(3)设![]() ),若函数
),若函数![]() 有三个零点,求实数
有三个零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校共有学生15 000人,其中男生10 500人,女生4500人.为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时).
(1)应收集多少位女生的样本数据?
(2)根据这300个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据的分组区间为:[0,2],(2,4],(4,6],(6,8],(8,10],(10,12].估计该校学生每周平均体育运动时间超过4小时的概率.

(3)在样本数据中,有60位女生的每周平均体育运动时间超过4小时,请完成每周平均体育运动时间与性别列联表,并判断是否有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() .
.
(1)若![]() 是
是![]() 的两个不同的根,是否存在实数
的两个不同的根,是否存在实数![]() ,使
,使![]() 成立?若存在,求
成立?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(2)设![]() ,函数
,函数![]() 已知方程
已知方程![]() 恰有3个不同的根.
恰有3个不同的根.
(ⅰ)求![]() 的取值范围;
的取值范围;
(ⅱ)设![]() 分别是这3个根中的最小值与最大值,求
分别是这3个根中的最小值与最大值,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log4(4x+1)+kx(k∈R)是偶函数.
(1)求k的值;
(2)设g(x)=log4![]() ,若函数f(x)与g(x)的图象有且只有一个公共点,求实数a的取值范围.
,若函数f(x)与g(x)的图象有且只有一个公共点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,边长为4的正方形![]() 与矩形
与矩形![]() 所在平面互相垂直,
所在平面互相垂直,![]() 分别为
分别为![]() 的中点,
的中点,![]() .
.

(1)求证:![]() 平面
平面![]() ;
;
(2)求证:![]() 平面
平面![]() ;
;
(3)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com