
(2010届枣庄市第一次调研)
已知函数f(x)对任意的实数x、y都有f(x+y) =f(x)+f(y)-1,且当x>0 时,f(x)>1.
(1)求证:函数f(x)在R上是增函数;
(2)若关于x的不等式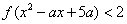 的解集为{x|-3<x<2=,求f(2009)的值;
的解集为{x|-3<x<2=,求f(2009)的值;
(3)在(2)的条件下,设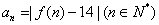 ,若数列
,若数列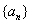 从第k项开始的连续20项 之和等于102,求k的值.
从第k项开始的连续20项 之和等于102,求k的值.
(1)证明:设x1>x2,则x1-x2>0,从而f(x1-x2)>1,即f(x1-x2)-1>0. ………2分
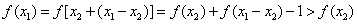 ,
,
故f(x)在R上是增函数.…4分
(2)设2 =f(b),于是不等式为 .
.
则 ,即
,即 .………6分
.………6分
∵不等式f(x2 -ax +5a) <2的解集为{x|-3<x<2},
∴方程x2-ax+5a-b=0的两根为-3和2,
于是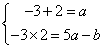 ,解得
,解得 ∴f(1)=2. ………8分
∴f(1)=2. ………8分
在已知等式中令x=n,y=1,得f(n+1)-f(n) =1.
所以{f(n)}是首项为2,公差为1的等差数列.
f(n)=2+(n-1)×1=n+1,故f(2009)=2010. ………10分
(3) 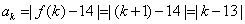 .
.
设从第k项开始的连续20项之和为Tk,则 .
.
当k≥13时,ak=|k-13|=k-13,Tk≥T13=0+1+2+3+…+19=190>102. (11分)
当k<13时,ak=|k-13|=13-k.
Tk=(13-k)+(12一k)+…+1+0+1+…+(k+6)=k2一7k+112.
令kk+112=102,解得k=2或k=5. ………14分
(注:当k≥13时,ak=|k一13|=k一13,令 ,无正整数解.得11分)
,无正整数解.得11分)


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com