

| A.上午10:00 | B.中午12:00 |
| C.下午4:00 | D.下午6:00 |
科目:高中数学 来源:不详 题型:解答题
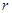 米,高为
米,高为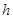 米,体积为
米,体积为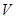 立方米.假设建造成本仅与表面积有关,侧面积的建造成本为100元/平方米,底面的建造成本为160元/平方米,该蓄水池的总建造成本为
立方米.假设建造成本仅与表面积有关,侧面积的建造成本为100元/平方米,底面的建造成本为160元/平方米,该蓄水池的总建造成本为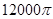 元(
元(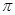 为圆周率).
为圆周率).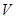 表示成
表示成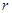 的函数
的函数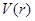 ,并求该函数的定义域;
,并求该函数的定义域;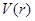 的单调性,并确定
的单调性,并确定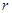 和
和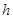 为何值时该蓄水池的体积最大.
为何值时该蓄水池的体积最大.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.25元 | B.20.5元 | C.15元 | D.12.5元 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 (a+b-|a-b|),如果函数f(x)=-x2+2x+3,g(x)=x+1,那么函数G(x)=F(f(x),g(x))的最大值等于________.
(a+b-|a-b|),如果函数f(x)=-x2+2x+3,g(x)=x+1,那么函数G(x)=F(f(x),g(x))的最大值等于________.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ,
, ,
, ,映射
,映射 .对于直线
.对于直线 上任意一点
上任意一点 ,
, ,若
,若 ,我们就称
,我们就称 为直线
为直线 的“相关映射”,
的“相关映射”, 称为映射
称为映射 的“相关直线”.又知
的“相关直线”.又知
 ,则映射
,则映射 的“相关直线”有多少条( )
的“相关直线”有多少条( )A. | B. | C. | D.无数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com