
(本小题14分)在奥运会射箭决赛中,参赛号码为1~4号的四名射箭运动员参加射箭比赛。
(Ⅰ)通过抽签将他们安排到1~4号靶位,试求恰有两名运动员所抽靶位号与其参赛号码相同的概率;
(Ⅱ)记1号、2号射箭运动员射箭的环数为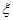 (
(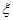 所有取值为0,1,2,3...,10)分别为
所有取值为0,1,2,3...,10)分别为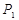 、
、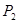 .根据教练员提供的资料,其概率分布如下表:
.根据教练员提供的资料,其概率分布如下表:
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
0 |
0 |
0 |
0 |
0.06 |
0.04 |
0.06 |
0.3 |
0.2 |
0.3 |
0.04 |
|
|
0 |
0 |
0 |
0 |
0.04 |
|
0.05 |
0.2 |
0.32 |
0.32 |
0.02 |
① 若1,2号运动员各射箭一次,求两人中至少有一人命中9环的概率;
② ②判断1号,2号射箭运动员谁射箭的水平高?并说明理由.
(Ⅰ)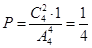
(Ⅱ)①p=1-0.476=0.524
②2号射箭运动员的射箭水平高.
【解析】本试题主要是考查了古典概型概率的运算,以及随机变量的分布列的求解和期望值的运用。
(1)、4名运动员中任取两名,其靶位号与参赛号相同,有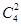 种方法,另2名运动员靶位号与参赛号均不相同的方法有1种,所以恰有一名运动员所抽靶位号与参赛号相同的概率为1/4
种方法,另2名运动员靶位号与参赛号均不相同的方法有1种,所以恰有一名运动员所抽靶位号与参赛号相同的概率为1/4
(2)由表可知,两人各射击一次,都未击中9环的概率为P=(1-0.3)(1-0.32)=0.476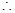 至少有一人命中9环的概率为p=1-0.476=0.524,那么利用各个取值概率值表示得到期望值,并比较大小得到水平高低问题。
至少有一人命中9环的概率为p=1-0.476=0.524,那么利用各个取值概率值表示得到期望值,并比较大小得到水平高低问题。
解(Ⅰ)从4名运动员中任取两名,其靶位号与参赛号相同,有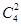 种方法,另2名运动员靶位号与参赛号均不相同的方法有1种,所以恰有一名运动员所抽靶位号与参赛号相同的概率为
种方法,另2名运动员靶位号与参赛号均不相同的方法有1种,所以恰有一名运动员所抽靶位号与参赛号相同的概率为 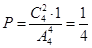
(Ⅱ)①由表可知,两人各射击一次,都未击中9环的概率为P=(1-0.3)(1-0.32)=0.476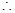 至少有一人命中9环的概率为p=1-0.476=0.524
至少有一人命中9环的概率为p=1-0.476=0.524
②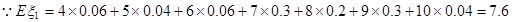
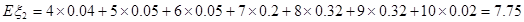
所以2号射箭运动员的射箭水平高.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2010年山东德州一中高一下学期模块检测数学卷 题型:解答题
(本小题14分)在平面直角坐标系中,O为坐标原点,已知向量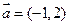 ,又有点
,又有点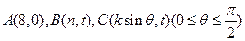
(1)若 ,且
,且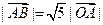 ,求向量
,求向量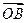 ;
;
(2)若向量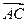 与向量
与向量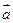 共线。当
共线。当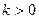 ,且函数
,且函数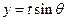 取最大值为4,求
取最大值为4,求 的值。
的值。
查看答案和解析>>
科目:高中数学 来源:2011年广东省揭阳市第一中学高二上学期期末检测数学文卷 题型:解答题
(本小题14分)在等比数列 中,
中, ,公比
,公比 ,且
,且 ,又
,又 与
与 的等比中项是2,
的等比中项是2,
(1)求数列 的通项公式;
的通项公式;
(2)设 ,数列
,数列 的前
的前 项和为
项和为 ,求
,求 .
.
查看答案和解析>>
科目:高中数学 来源:2010年山东德州一中高一下学期模块检测数学卷 题型:解答题
(本小题14分)在平面直角坐标系中,O为坐标原点,已知向量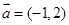 ,又有点
,又有点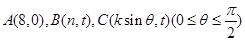
(1)若 ,且
,且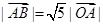 ,求向量
,求向量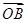 ;
;
(2)若向量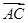 与向量
与向量 共线。当
共线。当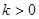 ,且函数
,且函数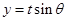 取最大值为4,求
取最大值为4,求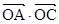 的值。
的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com