分析:因为在半径为15的球内有一个底面边长为
12的内接正三棱锥,故此三棱锥的高未定,根据球体的对称性可判断符合条件的正三棱锥有两个,分别考虑球心在三棱锥的高上还是在高外,求得三棱锥的高即可利用三棱锥体积公式计算结果
解答:解:如
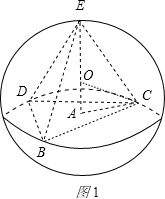
图
设球的球心为O,内接正三棱锥为E-BCD,
则三角形BCD为正三角形,边长BC=
12,外接圆半径AC=
× 12=12
球的半径OC=OE=15
(1)若E、A分别在球心O的两侧(如图1),则在Rt△OAC中,OA=
=
=9
∴正三棱锥为E-BCD的高EA=OE+OA=15+9=24
∴正三棱锥为E-BCD的体积
VE-BCD=×S△BCD ×EA=
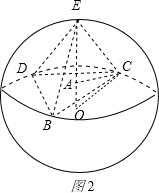
××(12)2×24=×108×24=864(2)若E、A分别在球心O的同侧(如图2),则
在Rt△OAC中,OA=
=
=9
∴正三棱锥为E-BCD的高EA=OE-OA=15-9=6
∴正三棱锥为E-BCD的体积
VE-BCD=×S△BCD ×EA=
××(12)2×6=×108×6=216故答案为
864或
216 点评:本题考查了球与三棱锥的接和切问题,球的性质,正三棱锥的性质及体积计算公式,空间想象能力,分类讨论的思想方法

 图
图 设球的球心为O,内接正三棱锥为E-BCD,
设球的球心为O,内接正三棱锥为E-BCD,
