
【探究】 解:设所求点D的坐标为(x、y),如图由于kAB=3,kBC=0,
∴kAB·kBC=0≠-1,
即AB与BC不垂直,
故AB、BC都不可作为直角梯形的直角边.
(1)若CD是直角梯形的直角边,
则 BC⊥CD,AD⊥CD.
∵kBC=0,∴CD的斜率不存在,从而有x=3.
又kAD=kBC,∴![]() ,即y=3.
,即y=3.
此时AB与CD不平行.
故所求点D的坐标为(3,3).
(2)若AD是直角梯形的直角边,则AD⊥AB,AD⊥CD.
∵kAD=![]() ,kCD=
,kCD=![]() ,
,
又由于AD⊥AB,∴![]() .
.
又AB∥CD,∴![]() .解上述两式可得
.解上述两式可得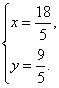
此时AD与BC不平行.
综上可知,使ABCD为直角梯形的点D的坐标可以为(3,3)和![]() .
.
【规律总结】 (1)把哪条边作为直角梯形的直角腰是分类的标准,解决此题时要注意不要丢下基础的东西.
(2)在遇到两条直线的平行或垂直的问题时,一是要注意直线的斜率不存在时的情形,如本例中的CD作为直角腰时,其斜率便不存在.


科目:高中数学 来源:2013届湖南省华容县高二第一学期期末考试理科数学试卷 题型:解答题
(本小题满分13分)已知A(0,2,3),B(-2,1,6),C(1,-1,5)
(1)求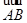 、
、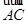 、
、 ;
;
(2)求以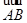 、
、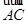 为边的平行四边形的面积;
为边的平行四边形的面积;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com