练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    10．已知两直线l1，l2的斜率恰是方程x2+bx-1=0的两实根，则l1，l2的位置关系是（　　）
    A．平行B．重合C．垂直D．无法确定

    分析 利用根与系数的关系、相互垂直的直线斜率之间的关系即可得出．

    解答 解：设直线l1、l2的斜率分别为k1，k2，
    ∵直线l1、l2的斜率是方程x2+bx-1=0的两根，∴k1k2=-1．
    ∴l1⊥l2．
    故选：C．

    点评 本题考查了根与系数的关系、相互垂直的直线斜率之间的关系，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    20．已知函数f（x）=xlnx-a（x-1），a∈R．
    （1）求曲线y=f（x）在点（1，f（1））处的切线方程；
    （2）当a＞0时，求证：f（x）在（0，a）上为减函数；
    （3）若当x≥1时，f（x）≥1恒成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

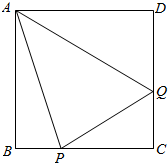    1．如图，某公司有一块边长为1百米的正方形空地ABCD，现要在正方形空地中规划一个三角形区域PAQ种植花草，其中P，Q分别为边BC，CD上的动点，∠PAQ=$\frac{π}{4}$，其它区域安装健身器材，设∠BAP为θ弧度．
    （1）求△PAQ面积S关于θ的函数解析式S（θ）；
    （2）求面积S的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．已知直线l：x-2y+m=0上存在点M满足与两点A（-2，0），B（2，0）连线的斜率kMA与kMB之积为-1，则实数m的取值范围是[-2$\sqrt{5}$，2$\sqrt{5}$]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．已知等差数列{an}的公差为d，等比数列{bn}的公比为q，且数列{bn}的前n项和为Sn．
    （1）若a1=b1=d=2，S3＜a1006+5b2-2016，求整数q的值；
    （2）若Sn+1-2Sn=2，试问数列{bn}中是否存在一点bk，使得bk恰好可以表示为该数列中连续p（p∈N，p≥2）项的和？请说明理由？
    （3）若b1=ar，b2=as≠ar，b3=at（其中t＞s＞r，且（s-r）是（t-r）的约数），证明数列{bn}中每一项都是数列{an}中的项．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

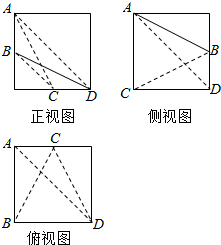    15．已知，棱长为2的正方体内有一内接四面体A-BCD，且B，C分别为正方体某两条棱的中点，其三视图如图所示：
    （Ⅰ）求证：AD⊥BC；
    （Ⅱ）求四面体A-BCD的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

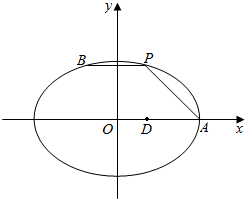    2．如图，在平面直角坐标系xOy中，已知点A为椭圆$\frac{{x}^{2}}{9}$+$\frac{2{y}^{2}}{9}$=1的右顶点，点D（1，0），点P，B在椭圆上，且在x轴上方，$\overrightarrow{BP}$=$\overrightarrow{DA}$．
    （1）求直线BD的方程；
    （2）已知抛物线C：x2=2py（p＞0）过点P，点Q是抛物线C上的动点，设点Q到点A的距离为d1，点Q到抛物线C的准线的距离为d2，求d1+d2的最小值．
    （3）求直线BD被过P，A，B三点的圆C截得的弦长；
    （4）是否存在分别以PB，PA为弦的两个相外切的等圆？若存在，求出这两个圆的方程；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．若x＞0，y＞0，xy=10，求x+3y的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．若2x-2-x=2$\sqrt{3}$，则2x+2-x=4．

    查看答案和解析>>

    同步练习册答案