一个正三棱柱有一个内切球(球与三棱柱的两个底面和三个侧面都相切)和一个外接球(球经过三棱柱的六个顶点),则此内切球、外接球与正三棱柱三个几何体的表面积之比为1: : .
【答案】
分析:设正三棱柱底面正三角形的边长为a,当球外切于正三棱柱时,球的半径R
1等于正三棱柱的底面正三角形的边心距,求出正三棱柱的高为,当球外接正三棱柱时,球的球心是正三棱柱中心高线的中点,且球的球心与正三棱柱两个底面正三角形构成两个正三棱锥,求出外接球的半径,即可求出内切球、外接球与正三棱柱三个几何体的表面积之比.
解答:解:设正三棱柱底面正三角形的边长为a,其内切球的半径为R
当球外切于正三棱柱时,球的半径R等于正三棱柱的底面正三角形的重心到对边的距离即R=
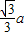
,到相对棱的距离是
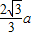
又正三棱柱的高是其内切球半径的2倍,故正三棱柱的高为

,
球外接正三棱柱时,球的球心是正三棱柱高的中点,且球的球心与正三棱柱两个底面正三角形构成两个正三棱锥,顶点在底面上的投影恰好是底面三角形的重心到顶点的距离
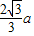
,棱锥的高为
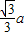
故正三棱锥外接球的半径满足
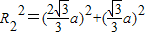
=

,
三棱柱的表面积为:

=

∴内切球、外接球与正三棱柱三个几何体的表面积之比4(π

):(4π

):

=R
2:R
22=1:5:
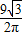
.
故答案为:5;
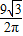
.
点评:本题是基础题,考查空间想象能力,分析问题解决问题的能力,是常考题型,求内切球与外接球的半径是本题的关键.

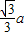 ,到相对棱的距离是
,到相对棱的距离是 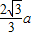
 ,
,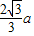 ,棱锥的高为
,棱锥的高为 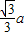
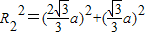 =
= ,
, =
=
 ):(4π
):(4π ):
): =R2:R22=1:5:
=R2:R22=1:5: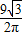 .
.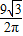 .
.
