
 种站法,然后其余5人在另外5个位置上作全排列有
种站法,然后其余5人在另外5个位置上作全排列有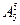 种站法,根据分步计数原理,共有站
种站法,根据分步计数原理,共有站

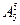 =480(种).
=480(种). 种站法,然后中间4人有
种站法,然后中间4人有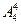 种站法,根据分步计数原理,共有站法
种站法,根据分步计数原理,共有站法

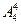 =480(种).
=480(种).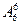 种法,甲在两端共有2
种法,甲在两端共有2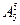 种站法,从总数中减去这两种情况的排列数,即得所求的站法数,共有
种站法,从总数中减去这两种情况的排列数,即得所求的站法数,共有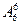
 2
2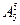 =480(种).
=480(种).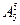 种站法,再把甲、乙进行全排列,有
种站法,再把甲、乙进行全排列,有 种站法,根椐分步计数原理,共有
种站法,根椐分步计数原理,共有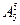

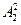 =240(种)站法.
=240(种)站法. 种;第二步再将甲、乙排在4人形成的5个空档(含两端)中,有
种;第二步再将甲、乙排在4人形成的5个空档(含两端)中,有 种,故共有站法为
种,故共有站法为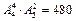 (种).
(种). 种站法,由(2)知甲、乙相邻有
种站法,由(2)知甲、乙相邻有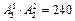 种站法,所以不相邻的站法有
种站法,所以不相邻的站法有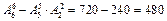 (种).
(种).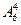 种,剩下的两个位置,左边的就是甲,右边的就是乙,全部排完,故共有
种,剩下的两个位置,左边的就是甲,右边的就是乙,全部排完,故共有 种.
种.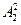 种,再让其他4人在中间位置作全排列,有
种,再让其他4人在中间位置作全排列,有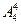 种,根据分步计数原理,共有
种,根据分步计数原理,共有

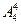 =48(种).
=48(种). 种站法,然后考虑中间4个位置,由剩下的4人去站,有
种站法,然后考虑中间4个位置,由剩下的4人去站,有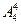 种站法,由分步计数原理共有
种站法,由分步计数原理共有

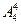 =48种站法.
=48种站法. 

科目:高中数学 来源:不详 题型:单选题
 ;乙列式子:
;乙列式子: ;丙列式子:
;丙列式子: ;丁列式子:
;丁列式子: ,其中列式正确的是
,其中列式正确的是 | A.甲 | B.乙 | C.丙 | D.丁 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.45 | B.55 | C.90 | D.100 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com