
| A. | (-∞,1]∪[3,+∞) | B. | [1,3] | C. | $[{\frac{3}{2},3}]$ | D. | $({-∞,\frac{3}{2}}]∪[{3,+∞})$ |
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
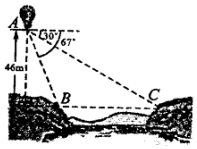 如图,从气球A上测得正前方的河流的两岸B,C的俯角分别为67°,30°,此时气球的高是46m,则河流的宽度BC约等于60m.(用四舍五入法将结果精确到个位.参考数据:sin67°≈0.92,cos67°≈0.39,sin37°≈0.60,cos37°≈0.80,$\sqrt{3}$≈1.73.
如图,从气球A上测得正前方的河流的两岸B,C的俯角分别为67°,30°,此时气球的高是46m,则河流的宽度BC约等于60m.(用四舍五入法将结果精确到个位.参考数据:sin67°≈0.92,cos67°≈0.39,sin37°≈0.60,cos37°≈0.80,$\sqrt{3}$≈1.73.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | lna>b-1 | B. | lna<b-1 | C. | lna=b-1 | D. | 以上都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com