
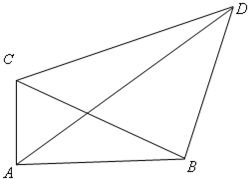
 如图,为了测不可到达的河北岸C,D之间的距离,在河南岸选定A,B两点,测得AB=100米,∠CAD=60°,∠DAB=30°,∠DBA=105°,∠CBA=45°,设A,B,C,D在同一个平面内,试求C,D两点之间的距离.
如图,为了测不可到达的河北岸C,D之间的距离,在河南岸选定A,B两点,测得AB=100米,∠CAD=60°,∠DAB=30°,∠DBA=105°,∠CBA=45°,设A,B,C,D在同一个平面内,试求C,D两点之间的距离. | AB2+AC2 |
| 1002×2 |
| 2 |
| BD |
| sin∠DAB |
| AB |
| sin∠ADB |
| 100×sin30° |
| sin45° |
| 2 |
| 6 |
| 6 |


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源:江苏省武进高级中学2008-2009学年度高一3月月考数学试题 题型:044
如图,为了测不可到达的河北岸C,D之间的距离,在河南岸选定A,B两点,测得AB=100米,∠CAB=60°,∠DAB=30°,∠DBA=120°,∠CBA=45°,设A,B,C,D在同一个平面内,试求C,D两点之间的距离.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com